Je me posais une question relative à la figure suivante :

A la base j'ai les trois points
Je souhaiterais déterminer
Auriez-vous des idées?
Merci d'avance

godzylla a écrit:c'est de la lumiere avec de l'éléctricité sans combustion.
il faut demander a des personnes qui vendent de la publicité et travaillent avec la nSa sur ces trucs, en attendant que certains mettent des images mathématiques.
comme cela ils savent ou sont les sites internet de mathématiques.
zygomatique a écrit:1/ comment insères-tu ton image ?
zygomatique a écrit:2/ homothétie + Thalès devrait le faire ....

chan79 a écrit:salut
Même en fixant les dimensions du triangle SBB1, ce n'est pas simple.
Si on prend SB=6 BB1=3 et SB1=5
Al Kashi donne
On nomme I le point d'intersection de (BB1) et (SS0)
On pose x=SA et y=SS0
Al Kashi dans SB1S0 donne
y²=x²- 10x/3 +9
Avec Thalès dans SBI (SI doit être égal à x), on obtient l'équation
on arrive à la valeur de x arrondie au millième à 4,996

chan79 a écrit:Pour les équations du quatrième degré, il y a bien la méthode Ferrari mais avec des paramètres, c'est pas la peine d'y penser.
Pour des valeurs approchées, c'est très rapide avec geogebra ou autres.
fluorhydrique a écrit:bonjour juste pour que des fois que ça peut servir un truc memo là ->
pour les equat des racines d'un poly du quatrieme degré
mais on peut toutefois faire un résumé de mémoire qui permet de les retrouver vite ci-dessous le resumé il est mnémotechnique beaucoup plus que ne le sont les équations qui donnent les racines
puis à partir de ce memo (en quatre parties ) finir par les écrire
on cherche un memo facile à se rappeler permettant de d'ecrire rapidement les racine d'un poly
je note en vert ce qui n'est pas important de se rappeler
mémo 1):
l'eq de translation
en posant la translation par t selon
bon là c'est pas la peine de l'écrire il suffit de dire qu'on a fait une translation de valeur t
mais je l'ecris quand mêmeok
on en deduit t,p,q,r
memo2)
on se rappellera que pour tout poly le lien entre les racines et les coefficients
tres facile à se rappeler
soit un poly de degré n definit par le (n+1) plet
bon là c'est pas la peine non plus de l'écrire
mais je l'ecris quand mêmeok
on considere le n-plet
en faitest la somme des
produit des u racines parmis les n racines
bon là c'est pas la peine non plus de l'écrire
mais je l'ecris quand mêmesomme des racines
produit des racines ok
pour u pair se rappeler le signe positif
pour u impair se rappeler le signe negatif
memo3)
la résolvante de la translation
on en deduit le système bon là c'est pas la peine non plus de l'écrire
mais je l'ecris quand mêmeok
en se rappelant de la formule somme et produit de deux réels on en deduit
avecdeux des racines de la resolvante
on trouve la somme
et la somme
puis on fait pareil même principe selon
on trouve le produit
et le produit
et avec ce qu'on a on se retrouve encore avec des sommes et produits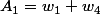
ect ...
et puis enfin
memo4)
se rappeler le cas particulier q=0 pas la peine de l'ecrire non plus
ça se base toujours sur le principe d'appliquer la formule sommes et produits
p=A+B et r=AB
selon
en espérant que comme ça on ai plus besoin de machines de logiciels et bref de plus rien et qu'on retourne faire du feu comme dans la guerre du feu pour se rechauffer dans des cavernes en compagnie de l'ours brun :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :