Bonjour,
Je suis bloqué sur un DM voici l'exo :
Une urne contient

boules blanches et une boule rouge. On tire successivement et avec remise 2 boules de l'urne.
On considère les évènements suivant :

: "Les deux boules sont de la même couleur"

:
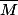
1) Calculer

et

pour

boules blanches
On considère le jeu suivant : le joueur perd
^2)
€ si

est réalisé et gagne
^2)
€ si

est réalisé. On appelle

la variable aléatoire égal au gain (positif ou négatif) du joueur.
2)
a Déterminer la loi de probabilité de

b Démontrer que
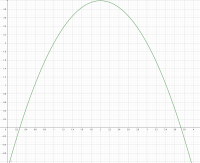
 = -n^2+4n-1)
c Pour quelles valeurs de

le jeu est favorable au joueur?
d Si on laisse choisir au joueur

que doit il répondre?
Pour le 1 tranquillou :

B La boule piochée est blanche
R La boule piochée est rouge
J'ai cet arbre :
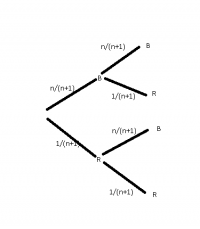
Je trouve alors
*P_B(B)+P(R)*P_R(R))
et
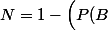*P_B(B)+P(R)*P_R(R)\Bigr))
donc
^2}+\dfrac{n^2}{(n+1)^2})
et
^2}+\dfrac{n^2}{(n+1)^2}\biggr))
pour le 2 c'est plus complexe :
Je ne sais pas quoi répondre pour le a

On est d'accord que
=X_1*P(X)_1+X_2*P(X)_2)
?
Merci de m'aider

“Placez votre main sur un poêle une minute et ça vous semble durer une heure. Asseyez vous auprès d'une jolie fille une heure et ça vous semble durer une minute. C'est ça la relativité.” Albert Einstein