Bonjour à tous alors je suis une étudiante au Québec au Canada. À ce que j'ai compris ce que nous étudions au Cegep vous étudier l'équivalent au lycée alors peut-être que vous serez en mesure de m'aider. Mon cours se nomme calcul différentiel et nous étudions les limites et dérivés. Voici le problème que je tente sans succès de résoudre :
Équation de l'ellipse : x2 + 4y2 = 4.
Les foyers : F= ( -√3 ; 0 ) et F ′ = ( √3 ; 0 )
À chaque point (x, y) sur l’ellipse, on peut associer un unique angle θ ∈ [0, 2π[ tel que
x = 2 cos(θ), y = sin(θ).
Ce paramètre θ s’appelle l’anomalie excentrique et est très connu en mécanique céleste pour étudier les orbites.
Vérifier par des calculs explicites que le point (2 cos(θ), sin(θ)) est bien sur l’ellipse ci-dessus et que le carré de la distance d’un point quelconque (x(θ),y(θ)) sur l’ellipse au point (1,0) est donné par la formule
f(θ) := d2((x, y), (1, 0)) = (2 cos(θ) − 1)2 + sin2(θ).
Trouver les points critiques de f qui sont situés dans l’intervalle [0, 2π[ et dessiner un tableau de
signe pour sa dérivée qui montre également la croissance de f entre les points critiques. ‡‡. Utiliser le fait (justifié dans la dernière partie du cours) que les dérivées de ces fonctions trigonométriques sont d sin(θ) = cos(θ) et d cos(θ) = − sin(θ). Dans ce problème, vous serez amenés à considérer deux angles 0 < α < π et
π < β < 2π qui satisfont cos(α) = cos(β) = 2/3. Puisqu’il n’est pas possible de trouver une formule explicite pour ces angles, vous pouvez simplement les appeler α, β dans le tableau de signe
Je ne sais pas si ça peut être utile, mais dans le numéro précédent j'ai calculer la dérivé implicite de l'ellipse qui est dy/dx=-x/4y
Calcul différenciel, ellipse, trigonométrie
7 messages
- Page 1 sur 1
Re: Calcul différenciel, ellipse, trigonométrie
bonsoir,
^2+4 sin^2(\theta)=4(cos^2 (\theta)+ sin^2(\theta))=4)
donc) appartient à l'ellipse.
appartient à l'ellipse.
,(1;0))^2=(2 cos \theta -1)^2+sin^2(\theta)=f(\theta))
=2(2cos(\theta)-1)(-2 sin(\theta))+2 sin(\theta)cos(\theta))
=-4\sin(2\theta)+4sin(\theta)+sin(2\theta))
=4\sin(\theta)-3sin(2\theta))
=2 sin(\theta) \left( 2-3cos(\theta) \right))
=0 \text{ ou } cos(\theta)=\frac{2}{3}))
on pose) et
et )
Cocotte13 a écrit:Vérifier par des calculs explicites que le point (2 cos(θ), sin(θ)) est bien sur l’ellipse ci-dessus
donc
le carré de la distance d’un point quelconque (x(θ),y(θ)) sur l’ellipse au point (1,0) est donné par la formule
f(θ) := d2((x, y), (1, 0)) = (2 cos(θ) − 1)2 + sin2(θ).
Trouver les points critiques de f qui sont situés dans l’intervalle [0, 2π[ et dessiner un tableau de
signe pour sa dérivée ..., vous serez amenés à considérer deux angles 0 < α < π et
π < β < 2π qui satisfont cos(α) = cos(β) = 2/3. Puisqu’il n’est pas possible de trouver une formule explicite pour ces angles, vous pouvez simplement les appeler α, β dans le tableau de signe
on pose
Re: Calcul différenciel, ellipse, trigonométrie
Salut @Mathelot ! Merci beaucoup pour ton aide. Si tu as le temps j’aimerais beaucoup si tu pouvais m’aider avec le reste de mon problème aussi. Le voici :
On cherche les points de l’ellipse qui sont les plus près du point (1,0). Par le problème 1, puisque la fonction x → x2 est strictement croissante si x ≥ 0, ceci revient à trouver les angles θ qui minimisent la fonction de distance au carré f. Trouver ces angles, puis en déduire que les coordonnées cartésiennes des points recherchés sont (4/3, ±√5/3).
Utiliser le résultat trouvé en b) pour trouver les équations des droites tangentes à l’ellipse aux deux points qui sont les plus près de (1, 0).
On cherche les points de l’ellipse qui sont les plus près du point (1,0). Par le problème 1, puisque la fonction x → x2 est strictement croissante si x ≥ 0, ceci revient à trouver les angles θ qui minimisent la fonction de distance au carré f. Trouver ces angles, puis en déduire que les coordonnées cartésiennes des points recherchés sont (4/3, ±√5/3).
Utiliser le résultat trouvé en b) pour trouver les équations des droites tangentes à l’ellipse aux deux points qui sont les plus près de (1, 0).
Re: Calcul différenciel, ellipse, trigonométrie
Bonjour, les points critiques sont donnés par @mathelot
A cause des symétries, on ne regardera que les points dont les angles sont dans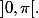
Il suffit de calculer f(0) et f(arccos(2/3)) pour voir que le point le + proche est donné par l'angle arccos(2/3). Maintenant cos(arcos(2/3))=2/3 et)=\sqrt{1-(2/3)^2 }) te donne les coordonnées cartésiennes du point. (Que j'appelle
te donne les coordonnées cartésiennes du point. (Que j'appelle ) pour la suite)
pour la suite)
Pour l'équation de la tangente il faut utiliser le résultat du b) mais c'est quoi ce résultat? (cette question b?)
Est ce que par hasard, cette question te permet de dire que la tangente en est perpendiculaire à
est perpendiculaire à 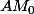 où A=(1,0)?
où A=(1,0)?
Si c'est le cas la tangente à pour équation :
.(\frac{1}{3},\frac{\sqrt{5}}{3})=0)
c'est à dire
A cause des symétries, on ne regardera que les points dont les angles sont dans
Il suffit de calculer f(0) et f(arccos(2/3)) pour voir que le point le + proche est donné par l'angle arccos(2/3). Maintenant cos(arcos(2/3))=2/3 et
Pour l'équation de la tangente il faut utiliser le résultat du b) mais c'est quoi ce résultat? (cette question b?)
Est ce que par hasard, cette question te permet de dire que la tangente en
Si c'est le cas la tangente à pour équation :
c'est à dire
Re: Calcul différenciel, ellipse, trigonométrie
Bonjour, @aviateur alors la réponse trouvé en b est dy/dx = -x/4y . Merci!
Re: Calcul différenciel, ellipse, trigonométrie
Bonjour
Alors je n'ai pas utilisé la question b. Néanmoins d'après la question b, on a
x dx +4 y dy=0 , c'est à dire qu'en tout point M=(x,y) de l'ellipse le vecteur (x, 4y) est un vecteur normal à la tangente. Pour ce vecteur est donc
ce vecteur est donc =4(1/3, 1 \sqrt{5}/3))
On retrouve bien le résultat que j'ai utilisé:) est orthogonal à la tangente en
est orthogonal à la tangente en 
Alors je n'ai pas utilisé la question b. Néanmoins d'après la question b, on a
x dx +4 y dy=0 , c'est à dire qu'en tout point M=(x,y) de l'ellipse le vecteur (x, 4y) est un vecteur normal à la tangente. Pour
On retrouve bien le résultat que j'ai utilisé:
Re: Calcul différenciel, ellipse, trigonométrie
re,
pour montrer l'existence d'un minimum de) , qui est de classe C2 (dérivée seconde continue), il suffit d'obtenir
, qui est de classe C2 (dérivée seconde continue), il suffit d'obtenir =0 , f''(\theta_0) > 0)
En effet, si f" est positive au voisinage de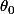 , f' est croissante, donc négative avant
, f' est croissante, donc négative avant 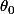 et positive au delà.
et positive au delà.
f est donc décroissante avant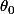 et croissante au delà. On a donc un minimum
et croissante au delà. On a donc un minimum
local en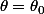 .
.
= 6 \left( -2 cos^2(\theta)+\frac{1}{2} cos(\theta)+1 \right))
il reste à vérifier le signe de f" en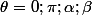
il vient:
<0 ; f"(\pi)<0; f"(\alpha)>0 ; f"(\beta)>0)
donc il y a deux minima locaux de f en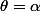 et
et 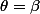
Ces minima sont globaux vû le tableau de variation de f.
autre point:
=\vec{AM(\theta)}.\vec{AM(\theta)}) (produit scalaire)
(produit scalaire)
=2 \vec{AM}.\frac{d}{d\theta} \vec{AM}(\theta)=0.)
La tangente en a une direction orthogonale au vecteur
a une direction orthogonale au vecteur 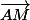
pour montrer l'existence d'un minimum de
En effet, si f" est positive au voisinage de
f est donc décroissante avant
local en
il reste à vérifier le signe de f" en
il vient:
donc il y a deux minima locaux de f en
Ces minima sont globaux vû le tableau de variation de f.
autre point:
La tangente en
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
