Calcul de coordonées

[L-Au-Ra]

Bonjour à tous !!!

J'ai une question à vous posez :$
J'ai un exercice à faire pour Demain

L'énoncer :

Soit les points :
A(-1.5;1) B ( 0.5 ; 2.5 ) C ( 3; 0.5) et D 1;-1)
a. Placez les points sur une figure
b. Démontrer que le quadrilatère ABCD est un parallélogramme.

J'ai déjà placer les points sur une figure.
Mais je suis bloqué pour la question b
Comment fait on pour démontrer que le quadrilatère est un parallélogramme dans ce genre d'exercice là ?

Merci D'avance à ceux qui essayerons de m'aider.

[Skrilax]

Quelles sont les différentes façons de prouver qu'un quadrilatère est un parallélogramme ?

[yvelines78]

bonjour,

A(-1.5;1) B ( 0.5 ; 2.5 ) C ( 3; 0.5) et D (1;-1)

ABCD //lo ça veut dire vectoriellement que vec AB=vecDC

vecAB(xb-xa;yb-ya)
vecDC(xc-xd;yc-yd)

des vecteurs = ont mêmes coordonnées

[L-Au-Ra]

Ben dans ma figure si AB = DC
ou si BC = AD
Alors c'est une parallélogramme je pense mais aprés faut le prouver que :
AB = DC
Ou
BC = AD

[Skrilax]

on peut également montrer que les côtés opposés sont parallèles deux à deux

Mais sinon, trouver la norme d'un vecteur est simple quand on connaît ses coordonnées

[L-Au-Ra]

bonjour,

A(-1.5;1) B ( 0.5 ; 2.5 ) C ( 3; 0.5) et D (1;-1)

ABCD //lo ça veut dire vectoriellement que vec AB=vecDC

vecAB(xb-xa;yb-ya)
vecDC(xc-xd;yc-yd)

des vecteurs = ont mêmes coordonnées

Donc je fais
vecAB(xb-xa;yb-ya)
vecDC(xc-xd;yc-yd)

Et si les vecteurs on les même coordonnées ABCD est un parallélogramme ?

[Skrilax]

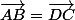
Tu as deux possibilités : soit tu prouves que (ou alors )

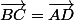
Ou bien tu prouves que AB // DC et BC // AB, et pour ça, tu montres que les vecteurs sont parallèles

[L-Au-Ra]

J'ai fais les calcul et je trouve

VecAB = ( 2.5;1.5)
VecDC = ( 2 ; 1.5 )

Mais les vecteurs n'ont pas exactement les même coordonnées je fais comment ? :$

[Skrilax]

Comment prouver que deux vecteurs sont parallèles, comment trouver la distance AB quand on a les coordonnées de ?

Je suis sûr que si tu ouvres ton cahier tu vas trouver

Les vecteurs n'ont pas les mêmes coordonnées parce que t'as fait une petite erreur de calcul :happy2:

[L-Au-Ra]

Okay merci beaucoup pour votre aide ;)