Calcul algébrique

[BloodRuru]

Bonjour, je ne comprends pas un exercice à propos de calcul algébrique, bien que j'ai trouvé les réponses à deux questions.

On se propose de résoudre le problème suivant: "Peut-on trouver un réel positif qui, une fois élevé au cube, a la même valeur que son double augmenté de 1 ?"

a) Vérifiez que résoudre le problème équivaut à résoudre: x^3-2x-1=0 avec x>0

b) Justifier que pour tout réel x: x^3-2x-1=(x+1)(x^2-x-1)
(Celle-ci j'ai réussi à la faire en développant.)

c) En déduire que résoudre le problème équivaut à résoudre: x^2-x-1=0 avec x>0

d) Justifier que pour tout réel x: x^2-x-1=(x-1/2)^2-5/4
(Celle-là aussi j'ai réussi avec les identités remarquables.)
En déduire la solution exacte du problème.

Donc voilà, je ne comprends pas la question a) et c), et je ne vois pas non plus comment en déduire la solution exacte du problème dans la question d), donc si quelqu'un voulait bien m'aider, merci d'avance.

[Ericovitchi]

trouver les solutions de x^3-2x-1=0 c'est trouver celles de (x+1)(x²-x-1)=0
et donc celle de x²-x-1=0 car on peut écarter la solution x=-1 puisque l'on cherche que des x>0

une fois sous la forme (x-1/2)²-5/4=0 il faut remarquer que c'est un A²-B² (en choisissant bien A et B et donc un (A+B)(A-B)=0
il ne suffit plus que d'annuler l'un ou l'autre facteur pour trouver les deux x solutions.

[BloodRuru]

Merci Ericovitchi,
mais en fait je ne comprends même pas comment résoudre la première equation avec un nombre au cube, et pour la question c), je vois pas comment faire non plus parce que j'ai pas l'impression qu'on puisse utiliser les identité remarquables pour enlever le carré.
Pour la d), je vois pas comment mettre au carré 5/4.
Donc je suis désolée, mais je ne comprends toujours pas ^^'

[Ericovitchi]

mais pour résoudre x^3-2x-1=0 tu résous (x+1)(x²-x-1)=0 puisque tu as montré que c'était pareil.
résoudre (x+1)(x²-x-1)=0 c'est annuler l'un ou l'autre des deux facteurs
x+1=0 donne x=-1 mais on écarte cette solution car x0
Reste à résoudre x²-x-1=0
Pour cela, l’énoncé t'aide en disant de la mettre sous la forme (x-1/2)²-5/4
qui est un A²-B² avec A=x-1/2 et B=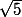/2 et qui se mets donc sous la forme (A+B)(A-B)=0
Et là pour trouver les deux solutions, tu vas à nouveau dire que pour que ça soit nul il faut que l'un ou l'autre des facteurs s'annule.

[BloodRuru]

D'accord, je comprends mieux. Donc pour la solution exacte du problème (dans la question d)), c'est x = racine carré de 5/2 ?
Mais par contre, pour répondre aux questions, t'utilises des infos de la question suivante, c'est pas grave ?

[Ericovitchi]

Donc pour la solution exacte du problème (dans la question d)), c'est x = racine carré de 5/2 ?

non pourquoi dis tu ça ?

(x-1/2)²-5/4= 0 c'est
Quels sont les x qui annulent l'un ou l'autre des deux facteurs ?
surement pas

[BloodRuru]

Les x-1/2 s'annulent ? Je suis désolée, mais j'ai jamais entendu parler des facteurs qui s'annulent, c'est pour ça que je comprends pas très bien.
Du coup, la solution doit être 1+racine5/2, puisque 1-racine5/2 est <0 et qu'on n'en a pas besoin ?