Bonjour.
Une première remarque : tu peut parfaitement laisser le résultat sous cette forme (a moins qu'on te demande explicitement de le simplifier)
Ensuite, il est utile de savoir que, la plupart du temps, ce genre de racine de racine ne se simplifie pas.
Pour ton cas particulier,

tu pourrait quand même factoriser 4 qui est un carré parfait :

.
Arrivé à ce point, si tu veut voir si "ca se simplifie", tu écrit que tu voudrait que

avec a et b "pas trop compliqués" car les solutions du type

et

ne constituent pas vraiment des simplifications !!!!!
Tu considère donc que tu aimerais trouver s'il y a des solutions avec a et b des entiers (ou des quotients).
En élevant au carré l'équation implique
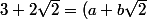^2=a^2+2b^2+2ab\sqrt{2})
ce qui est vrai si on a

et
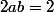
(si tu a vu que

est irrationnel, alors il est assez facile de montrer que c'est une équivalence).
Tout cela se termine par de l'arithmétique : peut tu trouver des entiers a,b tels que 2ab=2 et a²+2b²=3 ?
Si tu cherche un peu, tu verra que la réponse est oui et donc que dans ce cas particulier, la racine de racine se simplifie.
