Calcul d'aire de triangle en "toile d'araignée"
36 messages
- Page 2 sur 2 - 1, 2
Re: Calcul d'aire de triangle en "toile d'araignée"
...
Modifié en dernier par mathelot le 13 Jan 2022, 23:57, modifié 1 fois.
Re: Calcul d'aire de triangle en "toile d'araignée"
...
Modifié en dernier par mathelot le 13 Jan 2022, 23:58, modifié 1 fois.
Re: Calcul d'aire de triangle en "toile d'araignée"
Pourquoi modifies-tu ma citation ? Je parle bien de n+1 points en dimension n (3 dans le plan, 4 dans l'espace de dimension 3, etc. ) ou si tu préfères n en dimension n-1.
Les n+1 points sont les sommets d'un n-simplexe, en la formule donne le rapport du volume du petit simplexe (avec les sommets donnés par les évaluations ) à celui du gros simplexe (avec toutes les évaluations à 5).
) à celui du gros simplexe (avec toutes les évaluations à 5).
La formule vient tout simplement du fait qu'une transformation affine en dimension n modifie les n-volumes suivant le facteur donné par le déterminant de sa partie linéaire.
Les n+1 points sont les sommets d'un n-simplexe, en la formule donne le rapport du volume du petit simplexe (avec les sommets donnés par les évaluations
La formule vient tout simplement du fait qu'une transformation affine en dimension n modifie les n-volumes suivant le facteur donné par le déterminant de sa partie linéaire.
Re: Calcul d'aire de triangle en "toile d'araignée"
...
Modifié en dernier par mathelot le 13 Jan 2022, 23:58, modifié 1 fois.
Re: Calcul d'aire de triangle en "toile d'araignée"
On dirait que tu te trompes depuis le début : il s'agissait bien de trois points en dimension 2 !
Regarde le premier message : les triangles sont dans le plan.
Dans un espace affine de dimension n, un repère barycentrique est formé de n+1 points affinement indépendants.
Regarde le premier message : les triangles sont dans le plan.
graphique type "toile d'araignée" à trois axes -l'angle entre chaque axe est de 120°-;
Dans un espace affine de dimension n, un repère barycentrique est formé de n+1 points affinement indépendants.
Re: Calcul d'aire de triangle en "toile d'araignée"
...
Modifié en dernier par mathelot le 13 Jan 2022, 23:59, modifié 1 fois.
Re: Calcul d'aire de triangle en "toile d'araignée"
Mais les "axes" en question sont des demi-droites sur lesquels sont portés les évaluations, ce ne sont pas les axes d'un repère de l'espace ! Ce sont trois demi-droites dans un même plan.
Re: Calcul d'aire de triangle en "toile d'araignée"
GaBuZoMeu a écrit:Mais les "axes" en question sont des demi-droites sur lesquels sont portés les évaluations, ce ne sont pas les axes d'un repère de l'espace ! Ce sont trois demi-droites dans un même plan.
oh, purée !

Re: Calcul d'aire de triangle en "toile d'araignée"
De même, quand on aura quatre critères, 4 points affinement indépendants dans l'espace de dimension 3 qui sont les sommets d'un simplexe, avec les évaluations placées sur les demi-droite issues du centre de gravité du simplexe et allant vers les sommets. L'enveloppe convexe de ces quatre points donnés par les évaluations est un "petit" simplexe (éventuellement dégénéré si deux évaluations sont nulles), et on s'intéresse au rapport du volume du petit simplexe au grand simplexe.
Re: Calcul d'aire de triangle en "toile d'araignée"
lyceen95 a écrit:Si tu as besoin de ce coefficient k, il faut faire un peu de trigonométrie. Ca ne devrait pas résister plus de 3 minutes aux matheux qui traînent par ici.
Soient les points A,B,C,O dans le plan de la figure:
on a
d'où
aire(ABC)=aire(OAB)+aire(OAC)+aire(OBC)
L'aire maximale pour a=b=c=5 vaut
Le quotient de l'aire de ABC par l'aire maximale vaut
Modifié en dernier par mathelot le 14 Jan 2022, 10:21, modifié 1 fois.
Re: Calcul d'aire de triangle en "toile d'araignée"
La seule chose qui présente un intérêt est le rapport des deux aires, à mon avis.
Re: Calcul d'aire de triangle en "toile d'araignée"
Dans le dessin d'origine, les évaluations (5,0,0) et (4,0,0) conduisent à la même aire, ce qui peut être considéré comme un bug.
Re: Calcul d'aire de triangle en "toile d'araignée"
Pas si on décide que deux critères à zéro sont éliminatoires !
On peut travailler avec d'autres polynômes symétriques des évaluations, depuis la somme jusqu'au produit.
On peut travailler avec d'autres polynômes symétriques des évaluations, depuis la somme jusqu'au produit.
Re: Calcul d'aire de triangle en "toile d'araignée"
Merci à tous pour autant de réflexions et de brillance intellectuelle!
Avec ces éléments, j'ai reconstitué la formule Excel répondant à ma problématique sur 3 axes. Avec a=BC, b=AC et c=BA, j'associe la formule de Héron au théorème de Pythagore où a=sqr((B+Ccos60)²+(Csin60)²), b=sqr((C+Acos60)²+(Asin60)²) et c=sqr((C+Bcos60)²+(Bsin60)²), puis p=0.5*(a+b+c), donnant S par Héron.
Je garde sous le coude le sujet d'une étude sur 4 grandeurs et plus avec toutes vos remarques!
Avec ces éléments, j'ai reconstitué la formule Excel répondant à ma problématique sur 3 axes. Avec a=BC, b=AC et c=BA, j'associe la formule de Héron au théorème de Pythagore où a=sqr((B+Ccos60)²+(Csin60)²), b=sqr((C+Acos60)²+(Asin60)²) et c=sqr((C+Bcos60)²+(Bsin60)²), puis p=0.5*(a+b+c), donnant S par Héron.
Je garde sous le coude le sujet d'une étude sur 4 grandeurs et plus avec toutes vos remarques!
Re: Calcul d'aire de triangle en "toile d'araignée"
oui, tes formules sont exactes, elles peuvent encore se simplifier car cos(60°)=1/2 et sin(60°)=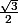
On trouve et les deux autres égalités par permutation circulaire.
et les deux autres égalités par permutation circulaire.
On trouve
36 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
