bonjour a tous
je suis en terminale economique et sociale
pouvais vous m'expliquer comment calculer la variance , la covariance et l'ecart type svp
qu'es ce que le shema de bernouilli
et a quoi et egal p (a sachant b) quand il sont dependant car je sais ( si je me trompe pas) que quand il sont independant sa fait p(a)*p(b)
p(b)
donc sa reviens a p(a) ...
Bonjour ; quelques explication a propos des probabilité et statistique
4 messages
- Page 1 sur 1
Bonjour,
1. calcul de la variance
2. calcul de l'écart-type
3. calcul de la covariance
4. schéma de Bernoulli
Ces 4 notions sont expliquées dans ton cours. Qu'est-ce que tu ne comprends pas précisément ?
Si A et B sont indépendants, alors :
P(A et B) = P(A).P(B)
P(A sachant B) = P(A)
P(B sachant A) = P(B)
Si A et B ne sont pas indépendants, alors on a la formule générale :
P(A et B) = P(A sachant B).P(B)
Nicolas
1. calcul de la variance
2. calcul de l'écart-type
3. calcul de la covariance
4. schéma de Bernoulli
Ces 4 notions sont expliquées dans ton cours. Qu'est-ce que tu ne comprends pas précisément ?
Si A et B sont indépendants, alors :
P(A et B) = P(A).P(B)
P(A sachant B) = P(A)
P(B sachant A) = P(B)
Si A et B ne sont pas indépendants, alors on a la formule générale :
P(A et B) = P(A sachant B).P(B)
Nicolas
Salut,
Esperance mathématique:
Soit une variable aléatoire X, definie sur un espace de probabilité}) .On appelle esperance mathematique de la variable X le nb réel E(X) défini par:
.On appelle esperance mathematique de la variable X le nb réel E(X) défini par:
}=\sum_{i=1}^{n}x_i\times{P(X=x_i)}=x_1P(X=x_1)+..+x_nP(X=x_n))
E(X) est la moyenne des valeurs prises par X, chaque valeur etant pondérée par sa probabilité.
De façon intuitive, E(X) représente la valeur moyenne que prendrait X si on repétait l'experience aléatoire un trés grd nb de fois.
Variance et écart type:
Pour une variable aleatoire X, dont l'esperance mathématique est E(X) on definit la variance de la variable aléatoire, noté V(X) par:
}=\sum_{i=1}^{n}(x_i-E(X))^2\times{P(X=x_i)})
on appelle ecart type de la variable aleatoire X, la racine carrée de la variance:
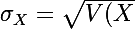})
on peut egalement calculer la variance par la formule:
}=\sum_{i=1}^{n}x_{i}^2P(X=x_i)-(E(X))^2)
exemple:
Un jeu consiste à lancer un dé cubique bien équilibré dont les faces portent les numéros 1,2,3,4,5,6.
On perd 1F si le numero est strictement inférieur à 5,on gagne 1 F si le numéro est 5, on gagne 5 F si le numero est6
1)Determiner la loi de probabilité de la variable X egale au gain algebrique.
Les valeurs prises par X sont :-1,1,5
donc
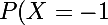}=P(\{1,2,3,4})=\frac{4}{6}) (on suppose l'equiprob.)
(on suppose l'equiprob.)
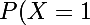}=P(\{5})=\frac{1}{6})
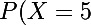}=P(\{6})=\frac{1}{6})
D'où la loi de probabilité de X:
tu fais le tableau habituel....
on peut calculer l'esperance de X:(on utilise la formule)
}=(-1)*\frac{2}{3}+1*\frac{1}{6}+5*\frac{1}{6}\approx{0,333})
on peut calculer la variance:
}=(-1)^2*\frac{2}{3}+1^2*\frac{1}{6}+5^2*\frac{1}{6}-(\frac{1}{3})^2=\frac{44}{9})
on en deduit l'ecart type:
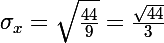
Schéma de Bernoulli:
Definition:
Soit 1 experience aléatoire fournissant comme resultat un evenement appelé succès (evenement S,de prob. p) ou bien un evenement appelé echec ( , de prob. q=1-p).
, de prob. q=1-p).
Si on realise successivement n fois cette experience, de façon independantes, on dit que l'on a un schéma de Bernoulli.
Exemple: on lance un dé cubique usuel et on s'intéresse à S="obtenir un numero au moins egal à 5".Si l'on repete ce lancer 10 fois on a un schéma de Bernoulli avec n=10.Si le dé est aprfait p=2/6=1/3 et q=2/3
Loi binomiale:
Lors d'une série de n epreuves aléatoires suivant un schéma de Bernoulli, on s'intéresse svt au nb de "succès" de l'épreuve".Ce nb de succés est une variable aléatoire X dependant des 2 paramètres:n(nb d'epreuves) et p(prob. du succès pour 1 epreuve).
Cette variable aléatoire X est appelée variable aléatoire binômiale;elle prend les valeurs 0,1,2..,n.Sa loi de probabilité est dite loi binômiale de probabilité et est donnée par la formule:
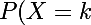}=C_n^{k}p^k(1-p)^{n-k}) k=0,1,..,n
k=0,1,..,n
cas particuliers frequents:
N'avoir aucun succès ds la serie de n epreuve: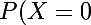}=(1-p)^n)
avoir n succès(c'est-à-dire uniquement des succès):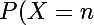}=p^n)
avoir au moins un succès:}=1-P(X=0)=1-(1-p)^n)
Covariance:
on appelle covariance des variables aléatoires X et Y la quantité notée, cov(X,Y), definie par:
}=E(X.Y)-E(X).E(Y))
Probabilités conditionnelles:
Def:
Soit B un evenement de probabilité non nul; la probabilité de l'evenement A sachant que B est réalisé est notée:}) ou
ou })
Par definition:
}=\frac{P(A\cap{B})}{P(B)}) avec P(B)#0
avec P(B)#0
j'espere que j'ai pu t'éclairer
A+
Esperance mathématique:
Soit une variable aléatoire X, definie sur un espace de probabilité
E(X) est la moyenne des valeurs prises par X, chaque valeur etant pondérée par sa probabilité.
De façon intuitive, E(X) représente la valeur moyenne que prendrait X si on repétait l'experience aléatoire un trés grd nb de fois.
Variance et écart type:
Pour une variable aleatoire X, dont l'esperance mathématique est E(X) on definit la variance de la variable aléatoire, noté V(X) par:
on appelle ecart type de la variable aleatoire X, la racine carrée de la variance:
on peut egalement calculer la variance par la formule:
exemple:
Un jeu consiste à lancer un dé cubique bien équilibré dont les faces portent les numéros 1,2,3,4,5,6.
On perd 1F si le numero est strictement inférieur à 5,on gagne 1 F si le numéro est 5, on gagne 5 F si le numero est6
1)Determiner la loi de probabilité de la variable X egale au gain algebrique.
Les valeurs prises par X sont :-1,1,5
donc
D'où la loi de probabilité de X:
tu fais le tableau habituel....
on peut calculer l'esperance de X:(on utilise la formule)
on peut calculer la variance:
on en deduit l'ecart type:
Schéma de Bernoulli:
Definition:
Soit 1 experience aléatoire fournissant comme resultat un evenement appelé succès (evenement S,de prob. p) ou bien un evenement appelé echec (
Si on realise successivement n fois cette experience, de façon independantes, on dit que l'on a un schéma de Bernoulli.
Exemple: on lance un dé cubique usuel et on s'intéresse à S="obtenir un numero au moins egal à 5".Si l'on repete ce lancer 10 fois on a un schéma de Bernoulli avec n=10.Si le dé est aprfait p=2/6=1/3 et q=2/3
Loi binomiale:
Lors d'une série de n epreuves aléatoires suivant un schéma de Bernoulli, on s'intéresse svt au nb de "succès" de l'épreuve".Ce nb de succés est une variable aléatoire X dependant des 2 paramètres:n(nb d'epreuves) et p(prob. du succès pour 1 epreuve).
Cette variable aléatoire X est appelée variable aléatoire binômiale;elle prend les valeurs 0,1,2..,n.Sa loi de probabilité est dite loi binômiale de probabilité et est donnée par la formule:
cas particuliers frequents:
N'avoir aucun succès ds la serie de n epreuve:
avoir n succès(c'est-à-dire uniquement des succès):
avoir au moins un succès:
Covariance:
on appelle covariance des variables aléatoires X et Y la quantité notée, cov(X,Y), definie par:
Probabilités conditionnelles:
Def:
Soit B un evenement de probabilité non nul; la probabilité de l'evenement A sachant que B est réalisé est notée:
Par definition:
j'espere que j'ai pu t'éclairer
A+
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
