Bon exercice de révision pour le BAC

[Dinozzo13]

Bonjour, je pose ici un exercice de BAC assez complet je trouve, puisqu'il aborde plusieurs notions en même temps. Bon entrainement :++:

Pour tout complexe , on pose : .
1°)a) Calculer .
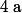
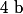
b) Déterminer les réels et tels que pour tout nombre complexe , on ait :

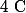
c) Résoudre dans l'équation : .
2°) Le plan complexe est rapporté à un repère orthonormal direct . On prendra pour unité graphique 2cm.
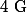
Soit et les points d'affixes respectives :
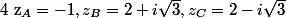
et .
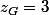
a) Placer ces points points sur un dessin.
b) En utilisant les nombres complexes, calculer les distances et .
En déduire la nature du traingle .
c) Calculer sous forme algébrique le nombre complexe .
En déduire la nature du triangle en justifiant soigneusement la réponse.
3°) Soit l'ensemble des points du plan tels que : .
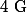
a) Vérifier que est le barycentre du système de points pondérés .
b) En déduire que la relation est équivalente à la relation : .
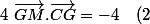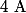
c) Vérifier que le point appartient à l'ensemble .
d) En déduire que la relation est équivalente à la relation : .
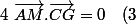e) En déduire l'ensemble et le tracer sur la figure précédente.

[bacha]

merci pour cette exercice et j'ai bien envie d'avoir un exercice sur les suite

[Dinozzo13]

Si tu veux ^^
J't'en met un tout de suite.

[Dinozzo13]

et sont deux réels tels que : . Les suites et sont définies par :
et, pour tout entier naturel : et .
1°) Montrer que, pour tout entier naturel : et sont strictement positifs.
2°) Montrer que, pour tout entier naturel : .
3°)a) Montrer que la suite est drécroissante.
b) Montrer que la suite est croissante.
4°)a) Montrer que, pour tout entier naturel : .
On pourra pour cela utiliser l'inégalité : ou tout autre méthode.
b) En déduire que, pour tout entier naturel : .
5°) En déduire de ce qui précède que les suites et convergent et ont la même limite.

Remarque : On dit que et , tels que définit au début de l'énoncé, sont les moyennes respectivement géométrique et arithmétique de et .

Bon travail !

[Dinozzo13]

Ou sinon il y a un topic que j'ai crée récemment sur les suites :
http://maths-forum.com/showthread.php?t=106330
Mais il n'est pas fini, il reste la partie B.
Si tu veux je te récapitule le début, ça t'évitera de voir la correction :

A. On considère la suite définie par et pour tout de : .
1°) Déterminer la solution de l’équation : .
2°) Montrer par récurrence que, pour tout de , .
Montrer que la suite est convergente et déterminer sa limite.
3°)a) Montrer que pour tout de ,.
b) Montrer à l’aide d’un raisonnement par récurrence que, pour tout de , .
En déduire une valeur approchée, par défaut, du nombre à près.