[Défi 3]: Bissectrice
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 25 Aoû 2012, 17:56
par Kikoo <3 Bieber » 25 Aoû 2012, 17:56
Je le peux

Dans un triangle quelconque, tu sais que son aire vaut :
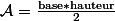
Donnons par exemple un triangle ABC quelconque. Soit AB=c; AC=b, BC=a
Nous avons de même les angles
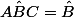
,
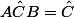
,
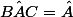
.
On sait que
=\frac{AH}{AB})
d'où une mesure de AH (la hauteur issue de A et orthogonale à (BC)) :
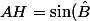\times AB)
Nous pouvons réécrire :
}{2}=\frac{ac\sin(\hat{B})}{2})
Par permutation circulaire, il vient
}{2}=\frac{bc\sin(\hat{A})}{2}=\frac{ab\sin(\hat{C})}{2})
Si on multiplie l'égalité précédente par 2 et qu'on la divise par abc, cela donne :
}{b}= \frac{\sin(\hat{A})}{a}=\frac{\sin(\hat{C})}{c})
qui est ce que l'on appelle "la loi des sinus".
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 25 Aoû 2012, 18:06
par chaa13 » 25 Aoû 2012, 18:06
Heu ... D'ou sait tu que
=\frac{AH}{AB})
Merci d'avance !!!!
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 25 Aoû 2012, 18:15
par Kikoo <3 Bieber » 25 Aoû 2012, 18:15
On travaille dans le triangle rectangle AHB ;)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 25 Aoû 2012, 18:24
par Lostounet » 25 Aoû 2012, 18:24
J'en connais une autre !
Tu prends un triangle quelconque ABC, et tu l'inscris dans un cercle (de diamètre d):

(Désolé, j'ai pas Java ici pour géogebra lol)

Avec les notations usuelles de a = BC
b = AC
c = AB
sin A' = a/d (triangle rectangle)
Alors sin A = a/d
Donc d = a/sinA
Tu fais de même pour C' = C (je te l'ai déjà placé), et tu trouves d = c/sinC
d = b/sin B
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 25 Aoû 2012, 18:30
par Kikoo <3 Bieber » 25 Aoû 2012, 18:30
Lostounet a écrit:J'en connais une autre !
Tu prends un triangle quelconque ABC, et tu l'inscris dans un cercle (de diamètre d):

(Désolé, j'ai pas Java ici pour géogebra lol)

Avec les notations usuelles de a = BC
b = AC
c = AB
sin A' = a/d (triangle rectangle)
Alors sin A = a/d
Donc d = a/sinA
Tu fais de même pour C' = C (je te l'ai déjà placé), et tu trouves d = c/sinC
d = b/sin B
Plus élégant

-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 25 Aoû 2012, 18:33
par chaa13 » 25 Aoû 2012, 18:33
A oui c'est la hauteur merci ! Par contre comment fais tu pour passer de BC*AB = AC ??
Quand tu parle de permutation circulaire cela veut dire que tu tourne le triangle de facon a changer de base, c'est ca ?
Merci d'avance !!!!!
EDIT : Je vien de voir vos deux poste
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 25 Aoû 2012, 18:38
par Kikoo <3 Bieber » 25 Aoû 2012, 18:38
chaa13 a écrit:A oui c'est la hauteur merci ! Par contre comment fais tu pour passer de BC*AB = AC ??
Quand tu parle de permutation circulaire cela veut dire que tu tourne le triangle de facon a changer de base, c'est ca ?
Merci d'avance !!!!!
EDIT : Je vien de voir vos deux poste
Non non, BC*AB=a*c, que je note ac...
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 25 Aoû 2012, 18:46
par chaa13 » 25 Aoû 2012, 18:46
Hey lostounet !!
Ca y'est jai compris ! Les deux méthode ! Juste une dernier question pour la méthode de Kikoo bieber : comment a tu obtenu le 2A/abc ? Comment le gars a trouver qu'il fallait multiplier par deux et diviser par abc ?????
Merci d'avance !!!!!!!!!!
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 25 Aoû 2012, 19:08
par Kikoo <3 Bieber » 25 Aoû 2012, 19:08
chaa13 a écrit:Hey lostounet !!
Ca y'est jai compris ! Les deux méthode ! Juste une dernier question pour la méthode de Kikoo bieber : comment a tu obtenu le 2A/abc ? Comment le gars a trouver qu'il fallait multiplier par deux et diviser par abc ?????
Merci d'avance !!!!!!!!!!
Ben ça arrangeait "le gars" de faire disparaitre le 2 en dénominateur et de faire apparaitre le côté opposé à l'angle ! Une manière de donner une relation facile à retenir et assez maniable lorsqu'on l'utilise

-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 25 Aoû 2012, 19:22
par chaa13 » 25 Aoû 2012, 19:22
Maintenant je vois merci !
Bon pour le B ... [TEX] Cos(180 - ALB)[/TEXT], Ok si les valeurs de n,p ou b sont différentes l'angle ALB sera différent, donc mon but serait de faire apparaître n, p ou n dans la formule ?
Merci d'avance !!!!

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 25 Aoû 2012, 21:15
par Lostounet » 25 Aoû 2012, 21:15
Hum...
180 - ALB , c'est en fait l'angle ALC...
Donc Al-kashi sur ALC pour pouvoir mettre en jeu b, p et n
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 25 Aoû 2012, 22:35
par chaa13 » 25 Aoû 2012, 22:35
Hey,
Je ne sais pas si c'est qui est demander de faire mais
)
ça fait l'angle ALB. Sinon que dois-je faire ?
Merci d'avance !!!!
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Aoû 2012, 20:12
par Kikoo <3 Bieber » 26 Aoû 2012, 20:12
chaa13 a écrit:Hey,
Je ne sais pas si c'est qui est demander de faire mais
)
ça fait l'angle ALB. Sinon que dois-je faire ?
Merci d'avance !!!!
Scuse pour le retard Chaa !
Nous avons
=\cos(\hat{ALC}))
et donc on n'a plus qu'à réappliquer Al Kashi dans le bon triangle

(Je ne fais que répéter Losti !)
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 30 Aoû 2012, 16:38
par chaa13 » 30 Aoû 2012, 16:38
Je suis désolé pour le gros retard !!Javoue que même si vous dites que l'exercice est guidée je suis asser perdu ... Je ne sais pas si c'est par rapport a mon niveau (Pourtant quand on a compris c'est plutôt simple) mais je ne sais pas trop quoi faire voyant les exercices !
Dans le C de quoi parle tu quand tu dis : "deux angles supplémentaire" ??
Merci d'avance !!!
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 12 Sep 2012, 15:25
par chaa13 » 12 Sep 2012, 15:25
Ca fait doublement longtemps ! Qui veut reprendre ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités

