Bijection entre deux ensembles finis

[Meepo]

Bonjour, svp aidez moi, j'ai peur, je bloque sur cet exo depuis un jour et j'ai sacrifié des heures de sommeil juste pour y penser.

Il faut que j'écrive la bijection entre deux ensembles et .

est l'ensemble de toutes les compositions de où chaque partie est un entier positif , càd , puis
, l'ensemble de toutes les compositions de où chaque partie est 1 ou 3,
càd .

On a déjà prouvé en cours que en passant par les séries, il s'agit maintenant de le démontrer avec une bijection.

Un élément de a un 'homologue' dans , qui est l'élément collé à . Ensuite, il faut trouver qqch pour les éléments de , mais je bloque.

Merci.

[zygomatique]

salut

c'est quoi une composition ?

[Meepo]

https://fr.wikipedia.org/wiki/Composition_(combinatoire)

Pardon, une composition d'un entierpositif est une façon de sommer l'entier avec des entiers positifs (il faut tenir compte de l'ordre). Ex. (4+1), (1+4),(3+1+1),... sont des compositions de 5...

[Ben314]

Salut,
Je pense que j'ai rien compris vu que ça me semble complètement contradictoire ton truc :

- Si Bn c'est l'ensemble des k-uplet (b_1,b_2,...,b_k) où les bi sont dans {1,3} et n=b1+b2+...+bk alors il me semble que, très clairement, le cardinal de Bn c'est celui de B(n-1) plus celui de B(n-3) [en disant que bk=1 ou (exclusif) bk=3]

- D'un autre coté, An est évidement vide si n n'est pas un multiple de 3 (vu que n ne risque pas de s'écrire comme une somme de multiples de 3) donc si le cardinal de Bn était systématiquement égal à celui de B(n-1) plus celui de An, ça signifierais qu'il est égal à celui de B(n-1) lorsque n n'est pas multiple de 3 et c'est clairement en contradiction avec le point précédent.

Est ce que tu peut donner une définition plus claire des Bn et des An et/ou donner explicitement la liste des élément de An,B(n-1) et B(n) par exemple pour n=7 ?

[Meepo]

Salut,

Pardon, il y avait une erreur dans la définition de An! >= 3, pas multiple de 3. Je viens de corriger l'énoncé.

Par exemple pour n =6, on a

A6: (6) et (3,3)
B5: (1,1,3) - (1,3,1) - (3, 1, 1) - (1, 1, 1, 1, 1)
B6: (1,1,3,1) - (1,3,1,1) - (3, 1, 1, 1) - (1, 1, 1, 1, 1, 1) - (1, 1, 1, 3) - (3,3).

c trop dur, trop dur...

[Ben314]

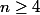
Il doit falloir supposer "un peu grand" pour que tout marche bien ( il me semble).

1) Le premier truc qui est complètement évident, c'est que l'application réalise une bijection de sur .

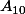
2) Reste à trouver une bijection de sur ce qui semble un peu plus délicat, mais en dressant par exemple la liste des 9 éléments de et de et en cherchant des "analogies" on trouve relativement facilement une solution :
Partant de on rajoute un 3 au début, puis on regroupe les termes en prenant un 3 plus tout les éventuels 1 qui suivent jusqu'au 3 suivant (ou jusqu'à la fin).
(1,3,1,1,3,3,1,3,1,1,1) -> (3,1,3,1,1,3,3,1,3,1,1,1) -> (3+1 , 3+1+1 , 3 , 3+1 , 3+1+1+1) = (4,5,3,4,6)
Et il est clair que l'opération en question est bien une bijection de sur (on écrit aisément la réciproque)

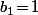
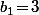
En plus, si on compose les bijection du 1) et du 2) (dans le cas où le premier terme est un 3), ça donne un truc simple : soit et on l'enlève, soit et on applique le "processus de regroupement" (et c'est pas la peine de rajouter le 3 au début vu que justement, il y est déjà...)