[Fonction composée] besoin d'un éclairage :)

[Roxfy]

Bonjour, je suis en révision de certains chapitres (je passe en terminale) et je suis tombé sur un exercice sur les fonctions composées, à priori tout bête, définir une fonction v o u (x). Il y'en a une qui n'avait pas de réponse et que j'ai voulu faire, comme ça.. Le problème c'est que je galère à trouver une réponse dont je suis sur :hum:

Voila, une composée de la forme v(x)= ax + b avec u(x)= x² est très simple à réaliser,
mais ici elle est de la forme v(x)= ax²-3x avec u(x)= x²

C'est le deuxième x qui m'embête, même si c'est surement très facile ça fait longtemps qu'on à fait les fonctions composées...

[Dinozzo13]

Salut !

Remplace tout simplement :

[Micki28]

Bonjour, je suis en révision de certains chapitres (je passe en terminale) et je suis tombé sur un exercice sur les fonctions composées, à priori tout bête, définir une fonction v o u (x). Il y'en a une qui n'avait pas de réponse et que j'ai voulu faire, comme ça.. Le problème c'est que je galère à trouver une réponse dont je suis sur :hum:

Voila, une composée de la forme v(x)= ax + b avec u(x)= x² est très simple à réaliser,
mais ici elle est de la forme v(x)= ax²-3x avec u(x)= x²

C'est le deuxième x qui m'embête, même si c'est surement très facile ça fait longtemps qu'on à fait les fonctions composées...

Bonjour,

Tu cherches v o u ?

v[u(x)] = a ( u(x) )² - 3 ( u(x) )

v(x) o u(x) = a (x²)² - 3x²

v(x) o u(x) = ax^4 - 3x²

Je pense que le mieux c'est de voir v o u comme v[u(x)]

PS: Mince, on m'a doublé !

[Dinozzo13]

Attention, je tiens tout de même à te rappeler la définition au cas où il y aurait des histoire de domaines ^^

Soient et deux fonction définies sur leur domaine respectifs 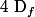et .
La fonction composée ( suivie de ) est définie si et seulement si et :
Ici il n'y a pas de problème avec ça car les deux fonctions sont définies sur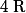
Pour tout de

[Dinozzo13]

Si tu veux un exemple concret :
Si tu prends et , ici il est très important de trouver el domaine de car cette fonction composée n'est pas assurément définie pour tout x réel

[Roxfy]

Et bien, c'est vraiment simple :marteau: je ne savais plus comment gérer le -3x, merci de vos réponses :)