soit f une fonction continue sur \left[0;1 \right]et derivable sur \left[0;1 \right]et verifiant f\left(0 \right)=f\left(1 \right)-\Pi/2
montrer qu il existe c\in \left[0;1 \right] telque \left(1+c \right)\acute{f}\left(c \right)=1/\sqrt{c}
je chcherche la fonction pour laquelle je dois utiliser roll et merci infinimen
Besoin d aide pour resoudre ce probleme
5 messages
- Page 1 sur 1
Re: Besoin d aide pour resoudre ce probleme
Bonjour
D'abord réédite ton message en ajoutant des balises [ tex].
Si j'ai bien interprété ton énoncé, commence par chercher une primitive de la fonction
de la fonction }) et applique le théorème de Rolle à la fonction
et applique le théorème de Rolle à la fonction 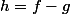 .
.
D'abord réédite ton message en ajoutant des balises [ tex].
Si j'ai bien interprété ton énoncé, commence par chercher une primitive
Re: Besoin d aide pour resoudre ce probleme
abraha11 a écrit:soit f une fonction continue sur
montrer qu il existe ctelque
je chcherche la fonction pour laquelle je dois utiliser roll et merci infinimen
C'est ça la question?
Re: Besoin d aide pour resoudre ce probleme
abraha11 a écrit:Soitune fonction continue et dérivable sur
telle que
.
Montrer qu'il existetel que
.
Essaye par exemple avec ça :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
