Besoin d'aide pour DM à rendre dem1 !!!!

par **nulenmath** » 18 Sep 2005, 15:02

bonjour j'ai un DM à rendre pour demain mais je ne sais pas du tout comment m'y prendre pour répondre aux premières question, si vous pouviez m'aider ça serait cool. voici l'énoncé ainsi que les questions :

A la surface d'une planète, dont l'accélération de la pesanteur est environ cinq fois moins forte que sur la Terre, d'une hauteur de 3 mètres, on lance un projectile vers le haut, à l'instant t = 0 avec une vitesse v.
La hauteur du projectile au-dessus du sol, à l'instant t, est donné par :
h(t)=-t²+vt+3, avec t supérieur ou égal à 0.
(unité du S.I. : t en secondes, v en m/seconde, h(t) en mètres.

1) Dans cette question, et seulement dans cette question, on prend v=1 m/s.
a) Déterminer la hauteur maximale de H atteinte. On pourra mettre h(t) sous forme canonique.
b) Déterminer l'instant t0, où le projectile atteint le sol.
c) Dans un repère orthonormal (0;i;j), représenter la fonction h sur [0;t0]

par **phenomene** » 18 Sep 2005, 15:15

nulenmath a écrit:bonjour j'ai un DM à rendre pour demain mais je ne sais pas du tout comment m'y prendre pour répondre aux premières question

Voilà qui est contradictoire : comment peux-tu n'en être qu'aux premières questions si le devoir est à rendre demain ? Il faut commencer par changer tes méthodes de travail et t'attaquer aux DM dès que tu en as l'énoncé...

par **nulenmath** » 18 Sep 2005, 15:30

merci bocoup pour ton aide ! j'apprécie énormément...
Si quelqu'un pourait m'aider vraiment ça serait sympa.

par **nulenmath** » 18 Sep 2005, 15:38

Y'a vraiment personne qui pourait m'indiquer une piste pour le a) ?

par **Nicolas_75** » 18 Sep 2005, 15:41

Comment fais-tu d'habitude pour trouver les extrema d'une fonction ?

(Remarque : tu peux également utiliser la forme canonique des expressions du 2nd degré)

par **phenomene** » 18 Sep 2005, 15:41

De rien. Cela me paraît plus utile de te donner une méthode de travail qui te permettra de réussir ton année (de première S, je suppose), que de faire un DM à ta place.

Maintenant, pour ton DM, qu'est-ce qui te pose problème ? Par exemple, pour la première question, on prend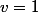

, donc

, expression qu'il s'agit de mettre sous forme canonique. Je suppose que tu as vu en cours la mise sous forme canonique d'un trinôme de degré deux, n'est-ce pas ?

Si tu précises ce que tu arrives à faire et ce qui te pose problème, tu auras de l'aide ; en revanche, poster un énoncé brut ne permet pas de t'aider...

par **nulenmath** » 18 Sep 2005, 15:49

j'ai trouvé la forme canonique de h(t) mais je ne sais pas comment m'en servir pour trouver la hauteur maximale H atteinte demandée dans le a).

par **Nicolas_75** » 18 Sep 2005, 15:56

Qu'as-tu trouvé comme forme canonique ?

par **nulenmath** » 18 Sep 2005, 15:59

h(t)=(t-1/-2)²+((1+12)/4)
elle est juste car j'aivérifé mais je ne sais pas à quoi elle peut me servir maintenant pour trouver la hauteur maximum de H. :cry:

par **Nicolas_75** » 18 Sep 2005, 16:02

Elle est fausse.
En développant, on devrait trouver un -

par **Nicolas_75** » 18 Sep 2005, 16:05

-

qui est maximum quand le carré est nul

par **nulenmath** » 18 Sep 2005, 16:06

pourtan quand je remplace t par 0 dans la formule de départ je trouve 3, et quand je remplace t par 0 dans la forme canonique que j'ai obtenu je trouve aussi 3. Tu es vraiment sur qu'elle est fausse ???

par **Nicolas_75** » 18 Sep 2005, 16:08

"pourtan quand je remplace t par 0 dans la formule de départ je trouve 3, et quand je remplace t par 0 dans la forme canonique que j'ai obtenu je trouve aussi 3."

Ce que tu dis est faux.

par **nulenmath** » 18 Sep 2005, 16:11

t'avais raison j'me suis trompé. en fait la forme canonique c'est :
h(t)=-1[(t+1/-2)²-(1+12)/4]
t'es d'accord ?

par **Nicolas_75** » 18 Sep 2005, 16:12

Euh... voir en haut de cette page.
Tu lis vraiment ce qu'on t'écrit ?

par **nulenmath** » 18 Sep 2005, 16:18

excuse j'avais pas vu.
mais pourquoi cette forme canonique est elle la hauteur H maximale quand le carré est nul ?

par **Nicolas_75** » 18 Sep 2005, 16:20

h(t) = 13/4 - nombre variable positif
h(t) est donc maximum quand ce "nombre variable positif" est nul, non ?

par **nulenmath** » 18 Sep 2005, 16:30

merci j'ai compris maintenant. je pense que je vais pouvoir me débrouiller maintenant mais juste une dernière question, dans la question "déterminer l'instant t0, où le projectile atteint le sol" il faut remplacer t par 0 ? ainsi on trouverait 3.

par **Nicolas_75** » 18 Sep 2005, 16:32

Non. Il faut trouver t tel que h(t)=0

par **nulenmath** » 18 Sep 2005, 16:34

donc en fait ça revient à trouver la ou les racines du polynôme ?

Besoin d'aide pour DM à rendre dem1 !!!!

besoin d'aide pour DM à rendre dem1 !!!!

Qui est en ligne