Besoin d'aide pour réduire une fraction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 27 Déc 2008, 17:35
par Gigi* » 27 Déc 2008, 17:35
Bonjour.
J'aurais besoin d'aide pour simplifier (x²+2x)/(x²+2x+1), cela fait plus d'une demi heure que j'essaie et je n'y arrive pas, il faut que je me rende à l'évidence, je ne sais plus simplifier une fraction =)
Si quelqu'un pouvait m'aider, merci ! ;)
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 27 Déc 2008, 17:36
par Billball » 27 Déc 2008, 17:36
x² + 2x= x(x+2)
x²+2x+1 = (x+1)²
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 27 Déc 2008, 17:41
par oscar » 27 Déc 2008, 17:41
Bonjour
C' est une fraction irréductible
-
sou71
- Membre Relatif
- Messages: 430
- Enregistré le: 05 Nov 2008, 17:51
-
 par sou71 » 27 Déc 2008, 17:47
par sou71 » 27 Déc 2008, 17:47
Sachant que x² + 2x = (x+1)² - 1
Et que x²+2x+1 = (x+1)²
^2-1}{(x+1)^2})
= 1 -
^2})
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 28 Déc 2008, 11:08
par Gigi* » 28 Déc 2008, 11:08
Merci beaucoup !
Mais en fait, j'ai mal expliqué mon problème...
Je dois calculer f ' (x) sachant que f(x)= x²/(x+1) et Df =[-1;2]
Je trouve donc f ' (x) = 2x(x+1) -1(x²)/(x+1)²
= 2x²+2x-x²/x²+2x+1
=x²+2x/x²+2x+1
Et c'est lorque j'arrive là que je n'arrive pas à donner lim
h->0
Merci d'avance ;)
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 28 Déc 2008, 11:26
par oscar » 28 Déc 2008, 11:26
Bonjour
lim ( x²+2x)/ ( x² +2x +1) si x--> O
cette limite = 0/1 = 0
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 28 Déc 2008, 20:15
par Gigi* » 28 Déc 2008, 20:15
C'est bien ce que je trouvais mais j'étais persuadée que ma réponse n'était pas la bonne. En tout cas, merci beaucoup !
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 28 Déc 2008, 20:54
par Gigi* » 28 Déc 2008, 20:54
J'ai encore un petit souci...
J'ai h(x)=cos2x -2sinx définie sur ]-pi ; pi ]
Je trouve h'(x)= -2sinx -2cosx , j'espère tout d'abord que ce résultat est juste ; ensuite, il faut que je trouve les valeurs de x pour lesquelles on a h'(x)=0.
Je bloque sur la méthode à employer...
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 28 Déc 2008, 21:21
par muse » 28 Déc 2008, 21:21
Gigi* a écrit:J'ai encore un petit souci...
J'ai h(x)=cos2x -2sinx définie sur ]-pi ; pi ]
Je trouve h'(x)= -2sinx -2cosx , j'espère tout d'abord que ce résultat est juste ; ensuite, il faut que je trouve les valeurs de x pour lesquelles on a h'(x)=0.
Je bloque sur la méthode à employer...
attention la dérivée de cos(2x) est -2sin(2x) et non pas 2sin(x)
donc la dérivée est bien h'(x)= -2sin(2x) -2cos(x)
Pour trouver les x tel que h'(x)=0:
-2sin(2x) -2cos(x)=0
+cos(x)=0)
cos(x)+cos(x)=0)
+1=0)
si cos(x)different de 0
=-\frac{1}{2})
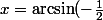=-0.5235987758)
maintenant si cos(x)=0 on a bien h' = 0or cos(x)=0 si x = +- Pi/2
donc il y a trois solution:
Pi/2
-Pi/2
=-0.5235987758)
Tout ça dans l'interval -pi ; pi
En image:

-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 28 Déc 2008, 23:19
par Gigi* » 28 Déc 2008, 23:19
Je ne vois pas comment on passe de sin(2x) + cos(x)=0 à 2sin(x)cos(x)+cos(x)=0
Et il y aussi la notion d'arc que je ne saisis pas...
Est que justufication graphique serait suffisante pour répondre à ce problème ?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 28 Déc 2008, 23:23
par Billball » 28 Déc 2008, 23:23
sin 2x = 2sinxcosx c'est une formule parmis tant d'autres de la trigo =)
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 28 Déc 2008, 23:31
par Gigi* » 28 Déc 2008, 23:31
Et on est censé l'avoir vu en 1ère S ?? Parce que là, ça commence vraiment à me faire peur ! :DD
En tout cas merci !
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 28 Déc 2008, 23:32
par Billball » 28 Déc 2008, 23:32
oui en 1ére S je l'ai vu et méme revu cette année en term!
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 28 Déc 2008, 23:35
par Gigi* » 28 Déc 2008, 23:35
J'ai beau relire mes cours, je vois pas cette formule donc ça me rassure, si je la connais pas, c'est pas de ma faute =)
Et encore une question (bête), c'est quoi arc ?
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 28 Déc 2008, 23:48
par Gigi* » 28 Déc 2008, 23:48
Là, je me rend compte que je pose des questions vraiment stupides...
arc sin, c'est sin -1...
:/
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 28 Déc 2008, 23:50
par Billball » 28 Déc 2008, 23:50
ué regarde ta calculette (si t'as la casio verte 35+ )
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 28 Déc 2008, 23:59
par muse » 28 Déc 2008, 23:59
Désolé pour l'arcsin j'aurais du préciser
Sinon pour la formule de trigo oui on les apprend en 1ère S maintenant tu ne les a peut etre pas encore vu.
Maintenant y'a 90% des élèves de TS ne connaissent pas les formules de trigo ...
A toi de bien les connaitre car elles peuvent se révéler très utile :)
-
Gigi*
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Déc 2008, 17:25
-
 par Gigi* » 29 Déc 2008, 00:21
par Gigi* » 29 Déc 2008, 00:21
Oui, c'est d'ailleurs en regardant ma calculatrice que j'ai eu le déclic ;)
Bon eh bien je vais tâcher de trouver toutes les formules concernant la trigo et de les apprendre ! =)
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 29 Déc 2008, 00:39
par muse » 29 Déc 2008, 00:39
ne les apprend pas n'importe comment y'a des méthode pour les retrouver...
En fait il me semble qu'il faut en connaitre 3/4 et les autres s'en déduisent.
Par contre me demande pas comment moi même je ne les connais pas :p ( a part les basique)
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 29 Déc 2008, 00:47
par Billball » 29 Déc 2008, 00:47
Gigi* a écrit:Oui, c'est d'ailleurs en regardant ma calculatrice que j'ai eu le déclic

Bon eh bien je vais tâcher de trouver toutes les formules concernant la trigo et de les apprendre ! =)
a savoir :
cos (a+b)_____L1
cos (a-b)_____L2
sin (a+b)_____L3
sin(a-b)_____L4
sin 2a_____(b=a dans L1)
cos 2a_____b=a dans L3)
cosa*cosb_____(L1+L2) / 2
sina*sinb_____(L2+L1) / 2
sina*cosb_____(L3+L4) / 2
cos²a
sin²a
sachant que si tu connais les 4 première, tu retrouves le reste
quand c'est cos [ cos (a+b) ou cos (a-b) ], tu récites co-co-si-si en inversant le signe
cos (a+b) =
cosa
cosb +
sina
sinb
cos (a-b) =
cosa
cosb -
sina
sinb
quand c'est sin [ sin (a+b) ou sin (a-b) ], tu récites si-co-co-si
sin (a+b) =
sina
cosb +
cosa
sinb
sin (a-b) =
sina
cosb -
cosa
sinb
allez bonne chance :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités

