Besoin d'aide pour un exercice sur suite et fonction (TS)

par **mathismylife** » 27 Oct 2015, 13:25

Bonjour je bloque sur la question 2 de mon exercice si quelqu'un pourrait m'aider :mur: :mur:

Donc voici une fonction compris dans l'intervalle ]-1 ; + infini[

f(x) = 3 - ((4)/(x+1))

U0 = 4
Un+1 = f(Un)

Pour la premiere question il faut montrer par recurence que Un est superieur ou égal à 1, pour tout n appartenant a grand N

Il faut montrer que f(x) est croussante sur R+ et en deduire que pour tout entier naturel n , on a Un+1 inferieur ou égal a Un

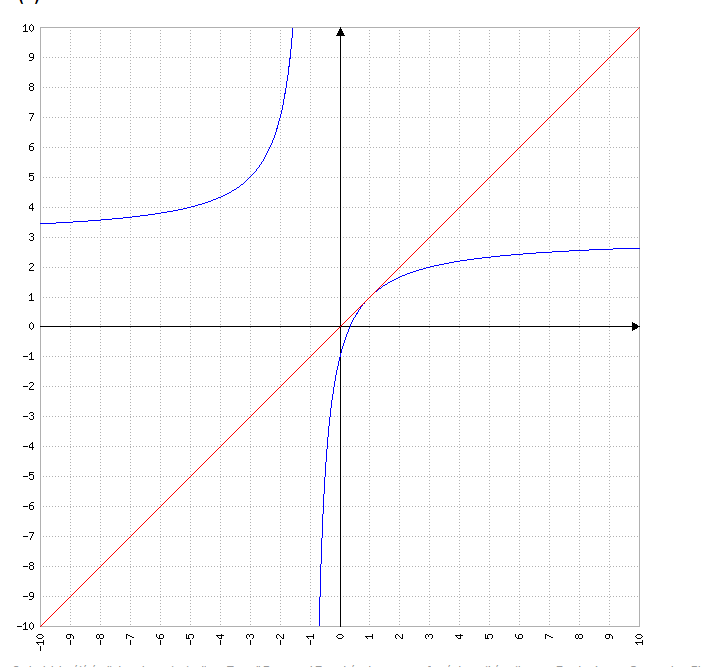
(j'ajoute aussi que sur le graphe la courbe bleue c'est f(x) et la courbe rouge c'est y=x )

Voila merci

par **mathismylife** » 27 Oct 2015, 13:38

L'exercice en question sur papier pour que ça soit plus compréhensible
Je bloque a la question 2 a et b si quelqu'un pourait m'aider en m'xpliquand ca serait gentil

par **titine** » 27 Oct 2015, 13:57

2a)
Initialisation :U(0) = 4 ;) 1

Hérédité :
On suppose que U(n) ;) 1
U(n+1) = f(U(n)) = 3 - 4/(U(n) + 1)
Si U(n) ;) 1 alors U(n) + 1 ;) 2
Donc 1/(U(n) + 1) ;) 1/2
Donc 4/((U(n) + 1) ;) 2
Donc -4/(U(n) + 1) ;) -2
Donc 3 - 4/(U(n) + 1) ;) 1

par **fenerbahcem23** » 27 Oct 2015, 15:53

Merci beaucoup j'avais trouvé cela mais javais oublié de changer le signe quand on rajoute le - :we: :ptdr:

par **fenerbahcem23** » 27 Oct 2015, 15:58

Pour la b j'ai fais cela

sur [0,+oo[ :
x est croissante
x+1 est croissante
1/(x+1) est décroissante
-1/(x+1) est croissante
-4/(x+1) est croissante
3-4/(x+1) est croissante

mais pour prouver que un+1 < Un comment je dois m'y prendre ?

par **nodjim** » 27 Oct 2015, 16:18

Calcule u(n+1)-un. Tu as besoin de connaitre le signe de 1+un pour résoudre l'inéquation, c'est pourquoi on te dit : "Déduire..".

par **mathismylife** » 27 Oct 2015, 19:02

nodjim a écrit:Calcule u(n+1)-un. Tu as besoin de connaitre le signe de 1+un pour résoudre l'inéquation, c'est pourquoi on te dit : "Déduire..".

Pour Un+1 - Un

Ca donne (si je me suis pas trompé)

3 - (4/Un+1) - Un

= (3Un-1/Un+1) - Un

= (Un² +4Un -1) / (Un +1)

c'est comme ca ?

Un +1 sera toujours positif car la suite commence par 4 et converge vers environ 1.25 (d'apres le graph)

par **mathismylife** » 28 Oct 2015, 13:39

Je ne vois pas comment faire y'a pas quelqu'un pour me débloquer svp ?

Besoin d'aide pour un exercice sur suite et fonction (TS)

Besoin d'aide pour un exercice sur suite et fonction (TS)

Qui est en ligne