Besoin d'aide pour un exercice sur les fonctions niveau term

[weezybaby]

PARTIE A: Etude d'une fonction auxiliaire
On considère la fonction g définie sur ]0;+infini[ par g(x)= x² + ln x
1. a) Montrer que g est strictement croissante sur ]0; +infini[
b) calculer g(1)

2. a) déduire de la question 1) les résultats suivants:
- si x supérieur ou égal à 1 alors x² + ln x est supérieur ou égal à 1
- si 0 < x inférieur ou égal à 1 alors x²+ln x est inférieur ou égal à 1
b) déterminer le signe de l'expression x²+ln x - 1 pour x appartenant à ]0;+infini[

PARTIE B: Etude d'une fonction
On considère la fonction f définie sur ]0;+infini[ par f(x)= x + 1 - (lnx / x)
on appelle (C) sa courbe représentative dans un repère orthonormal d'unité 2cm
1) Montrer que f'(x)= (x² + ln x - 1)/x²

2) en utilisant la partie A, donner le signe de f'(x) et dresser le tableau de variations de f sur ]0;+infini[

3) soit la droite delta d'équation y= x+1
Etudier la position relative de (C) par rapport à delta et préciser les coordonnées de leur point d'intersection I.

4) déterminer les coordonnées du point J de la courbe où la tangente (T) est parallèle à la droite delta

Merci d'avance :king2:

[capitaine nuggets]

Salut !

Un "bonjour" ne fait pas de mal ^^

Où bloques-tu ?

[weezybaby]

Bonjour ! Alors j'ai fais la question 1) le problème pour la 2a) c'est que je ne sais pas comment l'expliquer..
Ensuite je bloque a la question 1 de la partie B malgré que j'ai réussi a faire la question 2..

[capitaine nuggets]

Salut !

A : 2°)a) Si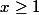 alors en élevant au carré des deux côtés ou en passant au logarithme des deux côtés .

Effectue alors la somme membre à membre des deux égalités obtenues :++:

Pareil lorsque .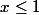

b : 1°) C'est un calcul tout bête de dérivée :lol3:

Prends ta fonction et met tout sous le même dénominateur.
est alors un quotient de fonctions utilise donc la formule donnant la dérivée d'un quotient de fonctions

[CENTER].[/CENTER]

[weezybaby]

Merci beaucoup mais pour le calcul de derivee je n'arrive toujours pas au résultat attendu..

[capitaine nuggets]

Ecris-moi sous forme de quotient.

Une fois cela fait, pose et .

Précise alors et .

Montre-moi alors ce que tu obtiens.