Besoin d'aide pour equation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 19 Juin 2007, 17:22
par keke43 » 19 Juin 2007, 17:22
SVP pouvez vous maider a resoudre cette equation en utilisant la factorisation et en mepliquant la methode ( on doit normalement trouver 2 solution ; 4xcarré-(x+1)carré= 0 merci
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 19 Juin 2007, 17:32
par annick » 19 Juin 2007, 17:32
Bonsoir,
Tu as dû voir les identités remarquables et c'est de la forme a²-b²=(a+b)(a-b)
A toi de bien définir a et b
Bon courage pour continuer
-
Enim
- Membre Naturel
- Messages: 62
- Enregistré le: 19 Juin 2007, 09:58
-
 par Enim » 19 Juin 2007, 18:10
par Enim » 19 Juin 2007, 18:10
Oui, on va utiliser les identités remarquable et voila comment :
4x²-(x+1)² = 0 <=> (2x-x-1) (2x+x+1) = 0
<=> (x-1) (3x+1) = 0 <=> (x-1 = 0) ou (3x+1 = 0) <=> (x = 1) ou (x = -1/3)
Finalement : Les solutions sont {-1/3;1} cest tout .
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 20 Juin 2007, 10:13
par keke43 » 20 Juin 2007, 10:13
merci bien mai les solution ne serai elle pas plutot ( 1 ; -1/3 ) dapré la reponse de tes calcul ?
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 20 Juin 2007, 10:14
par keke43 » 20 Juin 2007, 10:14
oubli se que jai dit javai mal lu mai merci vraiment maintenant jai compris :)
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 20 Juin 2007, 11:45
par oscar » 20 Juin 2007, 11:45
Bonjour
4x² - (x + 1 )² = 0
On applique la formule a ² - b² = (a - b) (a +b)
(2x)² - (x+1)²= 0
<=> [2x -(x+1)][2x + (x+1)]=0
<=>(2x - x - 1 )(( 2x + x +1)=0
<=> ( x -1) ( 3 x + 1) =0
=> x - 1 = 0 =>x' = 1
ou 3x +1 =0 => x" = -1/3 :id:
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 21 Juin 2007, 07:20
par keke43 » 21 Juin 2007, 07:20
merci bien es que tu pourrai me donner la formule de tte les identiter remarkable que tu connaisse me permetant de resoudre mieu mes equation ^^ merci davance
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 21 Juin 2007, 07:25
par fonfon » 21 Juin 2007, 07:25
salut, je pense que tu as dû voir ça au college
(a+b)²=a²+2ab+b²
(a-b)²=a²-2ab+b²
a²-b²=(a+b)(a-b)
tu peux aussi apprendre:
a^3+b^3=(a+b)(a²-ab+b²)
a^3-b^3=(a-b)(a²+ab+b²)
4ab=(a+b)²-(a-b)²
etc...
mais je crois que pour l'instant les 3eres te suffiront
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 21 Juin 2007, 07:54
par keke43 » 21 Juin 2007, 07:54
ok merci mais alors je voit vraiment pas comment je peu resoudre ceci :
(x^2+1)(4-3x)-8x+6x^2=0
merci et pourrai avoire la methode passque je compren pa gran chose la dedan merci :we:
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 21 Juin 2007, 08:06
par fonfon » 21 Juin 2007, 08:06
ok merci mais alors je voit vraiment pas comment je peu resoudre ceci :
(x^2+1)(4-3x)-8x+6x^2=0
merci et pourrai avoire la methode passque je compren pa gran chose la dedan merci
il arrive qu'il n'y ait pas toujours d'identité remarquable donc ici il faut faire apparaitre un facteur commun et factoriser
(4-3x)-8x+6x^2=0)
(4-3x)-2x(4-3x)=0)
(j'ai transformé -8x+6x² en -2x(4-3x) et donc j'ai fait apparaître un facteur commun qui est 4-3x donc maintenant on factorise par 4-3x afin de se ramener à qq chose du type
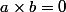
)
\times(x^2+1-2x)=0)
( j'arrange la derniere parenthèse)
\times(x^2-2x+1)=0)
( maintenant on recommait une identité remarquable ds x²-2x+1 c'est de la forme a²-2ab+b²=(a-b)²avec a=x et b=1 donc x²-2x+1=(x-1)²)
\times(x-1)^2=0)
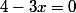
ou
^2=0)
je te laisse trouver les solutions
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 21 Juin 2007, 08:21
par keke43 » 21 Juin 2007, 08:21
eu ecuse moi mais comment resoudre (x-1)^2=0
jai essayer avc lidentité remarquable mais il me reste tjs un carré:
sa me donne : x^2+2x+1=0
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 21 Juin 2007, 08:23
par fonfon » 21 Juin 2007, 08:23
re,
resoudre (x-1)²=0 revient simplement à resoudre x-1=0 (en gros tu peux considerer que (x-1)²=0 <=> (x-1)(x-1)=0 c'est une solution double)
toi tu as redeveloppé ce qui ne faut surtout pas faire
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 21 Juin 2007, 08:25
par keke43 » 21 Juin 2007, 08:25
oula mais (x-1)(x-1) et loin detre egal a (x-1)
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 21 Juin 2007, 08:28
par fonfon » 21 Juin 2007, 08:28
(x-1)(x-1)=0 <=> (x-1)=0 ou (x-1)=0 donc x=1 ou x=1 c'est la même solution
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 21 Juin 2007, 08:30
par keke43 » 21 Juin 2007, 08:30
a daccord et ben merci bien !
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 21 Juin 2007, 08:34
par fonfon » 21 Juin 2007, 08:34
y-a pas de quoi :++:
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 21 Juin 2007, 08:35
par oscar » 21 Juin 2007, 08:35
Bonjour
Quand on considère x²- 2x + 1 = 0 ( <=> (x-1)²)
On peut calculer delta = (2)² - 4 =0
Il :happy2: a une racine "double" x' = x" = 2 / 2 = 1
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 21 Juin 2007, 08:38
par fonfon » 21 Juin 2007, 08:38
salut oscar, je ne pense pas que notre ami(e) ait vu le discriminant...
A+
-
keke43
- Membre Naturel
- Messages: 25
- Enregistré le: 19 Juin 2007, 17:14
-
 par keke43 » 21 Juin 2007, 10:07
par keke43 » 21 Juin 2007, 10:07
a vrai dire jai rien compri a ske ta dit oscar mais se netpa grave jai kan même reussit a comprendre la methode mai maintenant jaimerai vous demandez un probleme sur une inequation qui est : x(x+2)>0
dapré mon livre il y a 2solution pour moi les solution etai:
x>0 ou (x+2)>0
x>-2
mai eux ils trouve x>0 et x<-2
je ne voit pas ou es que lon change le signe ">" en "<"
merci
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 21 Juin 2007, 10:11
par fonfon » 21 Juin 2007, 10:11
re, tu peux te servir d'un tableau de signe ça te permettra mieux de voir l'ensemble des solutions
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
