Besoin d'aide pour dérivées
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 16:40
par LollYpoUp » 03 Déc 2006, 16:40
voila ,j'ai des exercices pour lesquelles la dérivé est importante.Comme j'ai peur de tout raté ,j'aimerai savoir la dérivée de
f(x)=x²* exp(x-1)-(x²/2)
et de
g(x)=(x+2)exp(x-1)-1
il faut aussi exprimer la derivé de f(x) en fontion de la fontion g(x)
Merci d'avance !
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 17:05
par Elsa_toup » 03 Déc 2006, 17:05
f est une somme de fonctions, donc sa dérivée est la somme des dérivées.
Dérivons

:
C'est un produit, donc sa dérivée sera
' e^{x+1} + x^2(e^{x+1})')
.
Ensuite -x²/2:
C'est une dérivée classique.
Sa dérivée sera
')
.
A toi de jouer !
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 17:32
par LollYpoUp » 03 Déc 2006, 17:32
Pourquoi obtient on x+1 alors que au depart c'etait x-1 pour l'exponentielle ?
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 17:35
par Elsa_toup » 03 Déc 2006, 17:35
Oui désolée: :error:
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 17:42
par LollYpoUp » 03 Déc 2006, 17:42
merci
Alor jobtient
2xexp(x-1)+x²*exp(x-1)-x
et si on factorise
(2+x)exp(x-1) -x ?
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 17:45
par Elsa_toup » 03 Déc 2006, 17:45
Oui c'est tout à fait ça, mais tu as oublié un x en factorisant ... (étourderie je suppose)
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 17:47
par LollYpoUp » 03 Déc 2006, 17:47
Nan je vois pas comment fair pour trouvé le 1 ...
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 17:50
par Elsa_toup » 03 Déc 2006, 17:50
Quel 1 ? On est toujours sur f, là, non ?
Je te dis juste que là :
2xexp(x-1)+x²*exp(x-1)-x
et si on factorise
(2+x)exp(x-1) -x
Tu as oublié le x.
Ca fait x(2+x)exp(x-1) - x.
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 17:51
par LollYpoUp » 03 Déc 2006, 17:51
euh oui oui jvien de le remarquer !
et maitenant pour G(x) je vois pas bien
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 17:57
par Elsa_toup » 03 Déc 2006, 17:57
Exactement le même principe.
C'est une dérivée de produit (le 1 dégage quand on dérive):
g'(x) = (x+2)' *
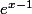
+ (x+2)*(
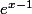
)'
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 18:01
par LollYpoUp » 03 Déc 2006, 18:01
pour g'(x)=exp(x-1)+(x+2)exp(x-1)
et faut trouver le rapport entre f'(x) et g(x)
mais je sais pas
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 18:03
par Elsa_toup » 03 Déc 2006, 18:03
f '(x) = x(2+x)exp(x-1) - x
et g(x)=(x+2)exp(x-1)-1.
Tu ne vois vraiment pas le lien ????
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 18:05
par LollYpoUp » 03 Déc 2006, 18:05
Ba comme ca de loin , je dirai que g(x) c'est la derivée de f'(x) donc al derivée seconde de f(x)
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 18:07
par Elsa_toup » 03 Déc 2006, 18:07
Tu vois pas que f '(x) c'est g(x) multiplié par quelque chose ????
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 18:11
par LollYpoUp » 03 Déc 2006, 18:11
Si par x !!!
j'ai oublier de te préciser que je rame pas mal en maths .. bien que je sois en term S
j'y suis seulement pour la svt
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 03 Déc 2006, 18:13
par Elsa_toup » 03 Déc 2006, 18:13
Ben tu l'as vu là pourtant.
C'est bien ça ! :++:
Du coup, en fait, au leiru de calculer g'(x) comme des barbares (moi la première), on pouvait écrire que g(x) = f '(x)/x et dériver g comme le quotient de deux fonctions...
(bon en même temps c'est pas franchement plus simple)
-
LollYpoUp
- Membre Naturel
- Messages: 34
- Enregistré le: 19 Avr 2006, 16:11
-
 par LollYpoUp » 03 Déc 2006, 18:19
par LollYpoUp » 03 Déc 2006, 18:19
Alors je ne vais pas me lancer dans ce calcul :doh:
Merci Beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
