bonjour à toutes et à tous
voilà je suis en classe de seconde et j'ai un DM en maths (manque que bol je suis nul ne maths)
j'ai réussit pratiquement tout le DM sauf l'exercice 3 qui est de la géométrie.
Je n'y comprend absolument rien à cet exercice ! j'aurais besoin d'aide. Merciiiiii d'avance et bonne
journée.
Voici l'exercice :
On considère la configuration si contre:
ABCD est un carré de côté 1.
BEFC est un rectangle.
Le triangle CFG est isocèle rectangle en G.
I est le milieu du segment [CF] et J celui du segment [BE].
On pose CF= 2a où a est un nombre réel
1) Conjecturer la nature du triangle GDE.
2) On souhaite démontrer cette conjoncture:
a. Justifier que G appartient au cercle de diamétre [CF].En déduire que IG=a
b. Exprimer la longueur DI en fonction de a.
En travaillant dans le triangle IDG,montrer que DG²=2a²+2a+1.
c. De la même façon,exprimer GE² et DE² en fonction de a.
d. Justifier alors la nature du triangle GDE.
Besoin d'aide je ne comprend absolument rien !!!
6 messages
- Page 1 sur 1
1)GDE est peut-ètre lui aussi isocèle rectangle, (comme CFG)
2)a
le triangle CFG est rectangle en G, donc que se passe-t-il avec son cercle circonscrit?
...
2)b
DI = DC + CI = 1 + 2a/2 = a+1
Pythagore dans le triangle rectangle DIG
(CGF est isocèle , la hauteur coupe CF au milieu)
DG² = DI² + IG² = (a+1)² + a² = ...
2)c
GE²
dans le triangle rectangle GJE
GE² = GJ² + JE² = ...
dans le triangle rectangle DEF
Pythagore,
donc DE²
d) justifie un peu ...
2)a
le triangle CFG est rectangle en G, donc que se passe-t-il avec son cercle circonscrit?
...
2)b
DI = DC + CI = 1 + 2a/2 = a+1
Pythagore dans le triangle rectangle DIG
(CGF est isocèle , la hauteur coupe CF au milieu)
DG² = DI² + IG² = (a+1)² + a² = ...
2)c
GE²
dans le triangle rectangle GJE
GE² = GJ² + JE² = ...
dans le triangle rectangle DEF
Pythagore,
donc DE²
d) justifie un peu ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Novice maths a écrit:Je ne comprend toujours pas la géomètrie c'est vraiment pas mon fort !!!
mais c'est pas de la géométrie, c'est un dessin avec des longueurs qui valent 1 ou a,
et ensuite avec Pythagore tu trouves les carrés
GE² = GJ² + JE² =
GJ c'est GI, c'est "a", puisque le rayon du cercle de diamètre CF + 1 le coté du carré est le petit coté du rectangle
GJ² = (a+1)²
JE est 2a/2= a
JE² = a²
GE² = (a+1)² + a²
développe ce truc identités remarquables
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Visiblement 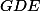 semble isocèle en
semble isocèle en . Le triangle
. Le triangle  est rectangle en
est rectangle en  Donc son cercle circonscrit a pour diamètre
Donc son cercle circonscrit a pour diamètre 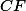 et donc
et donc 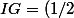CF=a.)
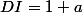 (évident)
(évident)
Dans le triangle rectangle on a
on a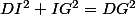 ; donc
; donc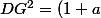^2+a^2=2a^2+2a+1.)
 se calcule dans le triangle rectangle
se calcule dans le triangle rectangle  on trouve :
on trouve : 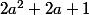
 se calcule dans le triangle rectangle
se calcule dans le triangle rectangle on trouve :
on trouve :^2=.....)
Conclusion: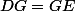 , mais
, mais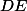 différent de
différent de , donc.....
, donc.....
Mais si on regarde mieux,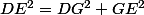 , donc....
, donc....
(Appliquer Pythagore, c'est quand même le minimum vital!!!)
Dans le triangle rectangle
Conclusion:
Mais si on regarde mieux,
(Appliquer Pythagore, c'est quand même le minimum vital!!!)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
