Bonjour,
J'ai une fonction h(x) définie sur l'intervalle
] -1 ; +infini [ par :
h(x) = (x^2 +3x+3)/(x+1)
On me demande de justifier que cette courbe admet une droite D pour asymptote oblique.
La question n'est pas de la calculée puisque le calcul de celle ci viens à la question suivante.
Par conséquent je ne sais pas comment justifier qu'une courbe admet une droite (D) pour asymptote oblique.
Pour la question qui suit je ne sais pas non plus comment calculer l'équation de cette asymptote.
BESOIN AIDE ASYMPTOTE OBLIQUE
2 messages
- Page 1 sur 1
Re: BESOIN AIDE ASYMPTOTE OBLIQUE
Bonjour;
On a : = \underset{x\rightarrow+\infty}{lim} \dfrac{x^2+3x+3}{x+1} =\underset{x\rightarrow+\infty}{lim} \dfrac{x^2}{x} =\underset{x\rightarrow+\infty}{lim} x = +\infty) ;
;
On cherche :}{x}=\underset{x\rightarrow+\infty}{lim} \dfrac{x^2+3x+3}{x^2+x}= \underset{x\rightarrow+\infty}{lim} \dfrac{x^2}{x^2}=1) ;
;
donc si l'asymptote oblique existe , alors son coefficient directeur est : 1 .
Il te reste à calculer son ordonnée à l'origine si il existe : - x) .
.
Une autre façon de faire et celle consistant à utiliser la transformation de Pisigma :
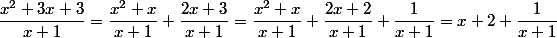 ;
;
donc on a : - (x + 2) = \dfrac{1}{x+1}) ;
;
donc : - (x + 2) = \underset{x\rightarrow+\infty}{lim} \dfrac{1}{x+1} = 0) ; d'où la conclusion .
; d'où la conclusion .
On a :
On cherche :
donc si l'asymptote oblique existe , alors son coefficient directeur est : 1 .
Il te reste à calculer son ordonnée à l'origine si il existe :
Une autre façon de faire et celle consistant à utiliser la transformation de Pisigma :
donc on a :
donc :
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
