bonjour,
pourriez-vous m'expliquer la loi de bernouilli à l'aide d'un exemple svp
merci et bonne journée.
Bernoulli + binomiale
5 messages
- Page 1 sur 1
par valentin.b » 11 Juin 2010, 23:24
Bonjour,
La loi de Bernoulli est vraiment simple. Elle donne la probabilité qu'a une expérience de donner un résultat "échec" ou "réussite" (je sais pas si c'est la bonne terminologie).
Par exemple, un lancer de pièce.
Si une variable aléatoire k suis cette loi, on code k=1 pour une réussite (un face par exemple), et k=0 pour un échec (donc pile). La loi de k est :
P(Face)=P(k=1)=1/2
P(Pile)=P(k=0)=1/2 (c'est à dire 1-1/2)
Autre exemple :
Un chasseur tire une fois sur un canard et le touche avec une probabilité p (qui tend vers 1 pour un bon chasseur). La variable aléatoire k qui suit la la de Bernouilli de paramètre p (On note : k suit la loi B(p)) et qui vaut 1 quand le chasseur tue le canard et 0 quand il le rate vérifie :
P(Canard plumé)=P(k=1)=p
P(Canard sauf)=P(k=0)=1-p
En fait on peut modéliser une unique expérience à deux issues par une loi de Bernouilli (enfin c'est l'idée).
La loi de Bernoulli est vraiment simple. Elle donne la probabilité qu'a une expérience de donner un résultat "échec" ou "réussite" (je sais pas si c'est la bonne terminologie).
Par exemple, un lancer de pièce.
Si une variable aléatoire k suis cette loi, on code k=1 pour une réussite (un face par exemple), et k=0 pour un échec (donc pile). La loi de k est :
P(Face)=P(k=1)=1/2
P(Pile)=P(k=0)=1/2 (c'est à dire 1-1/2)
Autre exemple :
Un chasseur tire une fois sur un canard et le touche avec une probabilité p (qui tend vers 1 pour un bon chasseur). La variable aléatoire k qui suit la la de Bernouilli de paramètre p (On note : k suit la loi B(p)) et qui vaut 1 quand le chasseur tue le canard et 0 quand il le rate vérifie :
P(Canard plumé)=P(k=1)=p
P(Canard sauf)=P(k=0)=1-p
En fait on peut modéliser une unique expérience à deux issues par une loi de Bernouilli (enfin c'est l'idée).
par ballas » 12 Juin 2010, 09:29
bonjour,
OK merci bien et la loi binomiale?
Car en faite, c'est parceque je suis en train de faire ca:
http://www.apmep.asso.fr/IMG/pdf/AmeriqueSudSpersonov2009.pdf
et j'essaie de comprendre la réponse à l'éxercice 4, question 1.b :
http://www.apmep.asso.fr/IMG/pdf/CorrigeSAmSuddecembre2009.pdf
merci et bonne journée.
OK merci bien et la loi binomiale?
Car en faite, c'est parceque je suis en train de faire ca:
http://www.apmep.asso.fr/IMG/pdf/AmeriqueSudSpersonov2009.pdf
et j'essaie de comprendre la réponse à l'éxercice 4, question 1.b :
http://www.apmep.asso.fr/IMG/pdf/CorrigeSAmSuddecembre2009.pdf
merci et bonne journée.
par valentin.b » 12 Juin 2010, 10:58
La loi Binomiale en fait c'est une répétition d'une même expérience de Bernouilli indépendante entre elles. La variable aléatoire K qui compte le nombre de succès et qui suis la loi de Bernouilli de paramètre p (probabilité de succès lors d'une expérience de Bernouilli) et n (nombre d'expérience de Bernouilli) vérifie :
 = \begin{pmatrix}<br />n \\<br />k<br />\end{matrix} p^{k} (1-p)^{n-k})
Par exemple avec la pièce, si on la lance n fois, la probabilité d'avoir k face, est :
 = \begin{pmatrix}<br />n \\<br />k<br />\end{matrix} {\frac{1}{2}}^{n})
Mais pour la pièce l'exemple est moins pertinant parce que :
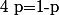
Prenons maintenant un exemple avec un dé. On dit qu'on a lancé le dé avec succès quand il donne "1", et qu'on a un échec sinon. On lance n fois le dé (chaque lancé est indépendant du précédent), et la probabilité d'avoir k succès (k "1") est :
 = \begin{pmatrix}<br />n \\<br />k<br />\end{matrix} \frac{1}{6^k}(\frac{5}{6})^{n-k}<br />=\begin{pmatrix}<br />n \\<br />k<br />\end{matrix} \frac{5^{n-k}}{6^n})
Normalement on retrouve la loi de Bernouilli quand n=1 :
 = \begin{pmatrix}<br />1 \\<br />k<br />\end{matrix} p^{k} (1-p)^{1-k})
Avec k égal à 1 ou 0 :
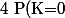 = \begin{pmatrix}<br />1 \\<br />0<br />\end{matrix} p^{0} (1-p)^{1}=1-p)
Et :
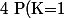 =\begin{pmatrix}<br />1 \\<br />1<br />\end{matrix} p^{1} (1-p)^{1-1}=p)
Par exemple avec la pièce, si on la lance n fois, la probabilité d'avoir k face, est :
Mais pour la pièce l'exemple est moins pertinant parce que :
Prenons maintenant un exemple avec un dé. On dit qu'on a lancé le dé avec succès quand il donne "1", et qu'on a un échec sinon. On lance n fois le dé (chaque lancé est indépendant du précédent), et la probabilité d'avoir k succès (k "1") est :
Normalement on retrouve la loi de Bernouilli quand n=1 :
Avec k égal à 1 ou 0 :
Et :
par ballas » 12 Juin 2010, 12:08
Merci pour le temps que tu as perdu pour moi, c'est sympa, j'ai compris.
Bonne journée!
Bonne journée!
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :