Barycentres
20 messages
- Page 1 sur 1
Barycentres
Bonjour,
Soit A le barycentre de (B;-2) et (C;5)
a) Determiner 2 réel x et y sachant que x + y = 6 et que le point B est le barycentre de (C;x) et (A;y).
b) Determiner 2 réels z et t sachant que z + t = 3 et que le point C est le barycentre de (A;z) et (B;t).
Merci !
Soit A le barycentre de (B;-2) et (C;5)
a) Determiner 2 réel x et y sachant que x + y = 6 et que le point B est le barycentre de (C;x) et (A;y).
b) Determiner 2 réels z et t sachant que z + t = 3 et que le point C est le barycentre de (A;z) et (B;t).
Merci !
A-
- On sait que A est le barycentre de (B ; -2) et (C ; 5).
On peut donc écrire que -2MB-> + 5MC-> = 3MA->
- On sait aussi que B est le barycentre de (C ; x) et de (A ; y).
On peut donc écrire que xMC-> + yMA-> = (x + y)MB->
Or x + y = 6 donc xMC-> + yMA-> = 6MB->
Après il suffit de mettre en rapport les deux équations qui mettent en rapport les mêmes vecteurs :
-2MB-> + 5MC-> = 3MA->
<=> 6MB-> = 15MC-> - 9MA->
Or 6MB-> = xMC-> + yMA->
Donc 15MC-> - 9MA-> = xMC-> + yMA->
D'où x = 15 et y = -9
B -
Le principe est exactement le même, je te donne la réponse pour que tu puisses vérifier : t = 6/5 et z = 9/5
Si tu as des questions, n'hésite pas !
- On sait que A est le barycentre de (B ; -2) et (C ; 5).
On peut donc écrire que -2MB-> + 5MC-> = 3MA->
- On sait aussi que B est le barycentre de (C ; x) et de (A ; y).
On peut donc écrire que xMC-> + yMA-> = (x + y)MB->
Or x + y = 6 donc xMC-> + yMA-> = 6MB->
Après il suffit de mettre en rapport les deux équations qui mettent en rapport les mêmes vecteurs :
-2MB-> + 5MC-> = 3MA->
<=> 6MB-> = 15MC-> - 9MA->
Or 6MB-> = xMC-> + yMA->
Donc 15MC-> - 9MA-> = xMC-> + yMA->
D'où x = 15 et y = -9
B -
Le principe est exactement le même, je te donne la réponse pour que tu puisses vérifier : t = 6/5 et z = 9/5
Si tu as des questions, n'hésite pas !
On a trouvé ces deux équations :
1 -\vec{MB} + 5\vec{MC} = 3\vec{MA})



2 -\vec{MB})
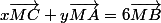 (puisque x+y = 6)
(puisque x+y = 6)
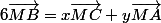
Soit les deux équations "modifiées" :
1 -
2 -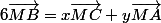
Donc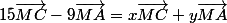
Tu remarques qu'il y a les mêmes vecteurs de chaque côté de l'équation donc les coefficients de ces vecteurs doivent êtres égaux. Or le coefficient du vecteur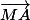 est -9 du côté gauche et y du côté droit. D'où y = -9.
est -9 du côté gauche et y du côté droit. D'où y = -9.
Idem avec x.
J'espère avoir éclairé ta lanterne mais si ce n'est pas le cas je peux essayer d'expliquer autrement si tu veux ^^
1 -
2 -
Soit les deux équations "modifiées" :
1 -
2 -
Donc
Tu remarques qu'il y a les mêmes vecteurs de chaque côté de l'équation donc les coefficients de ces vecteurs doivent êtres égaux. Or le coefficient du vecteur
Idem avec x.
J'espère avoir éclairé ta lanterne mais si ce n'est pas le cas je peux essayer d'expliquer autrement si tu veux ^^
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
