Bonsoir,
Il me faudrait une petite vérification de mes réponses pour un exercice de mon DM de maths sur les barycentres :
Enoncé :
SABCD une pyramide à base carrée ABCD,
Le point O est le centre du carré ABCD et le point G est l'isobarycentre de S,A,B,C,D.
Montrer que G appartient au segment [OS] et préciser la position du point G.
Mes réponses :
Le point O est le centre du carré ABCD, comme le centre d'un carré est déterminer par le point d'intersection des diagonales, on peut dire que O est l'isobarycentre de {(A;1)(B;1)(C;1)(D;1)}
On a G barycentre de {(A;1)(B;1)(C;1)(D;1)(S;1}
On prend H isobarycentre de {(A;1)(B;1)(C;1)(D;1)} (Je ne sais pas si j'ai le droit de prendre H barycentre partiel de 4 points... :hein: )
Donc G barycentre de {(H;4)(S;1)}
Or H=O, donc G barycentre de {(O;4)(S;1)}
Ainsi G appartient à [OS]
On en déduit que (ce sont des vecteurs) OG= 1/4+1 x(OS)
Ce qui me pose surtout problème, c'est le barycentre partiel H, est ce que je peux prendre 4 point et le remplacer par O ? Et pour préciser la postion, ma réponse me semble courte...
Merci d'avance pour votre aide. :we:
DM barycentres
4 messages
- Page 1 sur 1
Bonsoir,
Tu peux prendre un barycentre partiel dautant de points que tu veux tant que la somme de leurs coefficients nest pas nulle.
Je te propose une rédaction un peu mieux selon moi :
 étant le centre du carré
étant le centre du carré 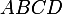 ,
,  est l'isobarycentre de
est l'isobarycentre de 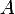 ,
, 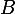 ,
, 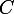 et
et  . (Tu ne dois pas donner les coefficients des points pondérés lorsque tu parles disobarycentre.)
. (Tu ne dois pas donner les coefficients des points pondérés lorsque tu parles disobarycentre.)
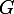 est lisobarycentre de
est lisobarycentre de 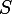 ,
, 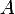 ,
, 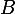 ,
, 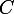 et
et  ; doù
; doù ;(A,1);(B,1);(C,1);(D,1) \right}) .
.
Soit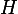 le barycentre partiel de
le barycentre partiel de ;(B,1);(C,1);(D,1)) .
.
Par associativité,;(H,4)\right}) .
.
Or, daprès la définition du point ,
,  . Doù
. Doù ;(O,4)\right}) .
.
On a ainsi : ou
ou  .
.
Conclusion :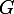 appartient au segment
appartient au segment  et
et 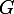 se situe aux
se situe aux 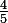 de
de  en partant de
en partant de 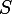 ou au
ou au  en partant de
en partant de  .
.
Tu peux prendre un barycentre partiel dautant de points que tu veux tant que la somme de leurs coefficients nest pas nulle.
Je te propose une rédaction un peu mieux selon moi :
Soit
Par associativité,
Or, daprès la définition du point
On a ainsi :
Conclusion :
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
