Barycentre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 14:29
par morgan88700 » 21 Jan 2010, 14:29
A et B sont deux points distinct du plan.
Determiner l'ensemble des points M tels que || 3MA -5MB||=||MA+MB ||
MA et MB sont des vecteurs
Merci de votre aide , je ne sais pas par quoi commencer
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 14:36
par Dinozzo13 » 21 Jan 2010, 14:36
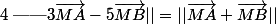
Pour commencer, il faut réduire les sommes

et

.
Pour réduire

, utilise le barycentre G de (A,3),(B,-5)

, introduit le point I milieu de [AB].
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Jan 2010, 14:40
par Doraki » 21 Jan 2010, 14:40
Bof.
Je préfère dire que ||u|| = u.u, et réécrire la condition avec des produits scalaires, du MA, et du AB.
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 14:45
par morgan88700 » 21 Jan 2010, 14:45
Je ne vois pas pourquoi tu veux introduire le point I ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 14:48
par Dinozzo13 » 21 Jan 2010, 14:48
Bah si tu introduit un isobarycentre G' de A et B, G' est le milieu de AB.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 14:49
par Dinozzo13 » 21 Jan 2010, 14:49
Doraki a écrit:Bof.
Je préfère dire que ||u|| = u.u, et réécrire la condition avec des produits scalaires, du MA, et du AB.
Ouais mais il n'a peut-être pas vu encore le produit scalaire.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 15:00
par Dinozzo13 » 21 Jan 2010, 15:00
D'après la propriété fondamentale, pour tout point M du plan :
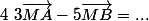
De même :
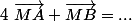
Ensuite, tu dis que :
M appartient à cet ensemble si et seulement si
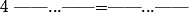
, tu en déduis une égalité et donc l'ensemble recherché.
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 15:31
par morgan88700 » 21 Jan 2010, 15:31
D'apres la proprioté fondamentale je trouve :
3MA-5MB = ( 3-5)MG
= -2MG
MA+MG = 2MG
Mais comme ||-2MG||=||2MG|| C'est pas cohérent ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 15:50
par Dinozzo13 » 21 Jan 2010, 15:50
Déjà,

ensuite, prend I milieu de [AB], tu as donc
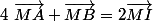
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 15:59
par morgan88700 » 21 Jan 2010, 15:59
Donc sa ferait
||-2MG||=||2MI|| ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Jan 2010, 16:01
par Doraki » 21 Jan 2010, 16:01
Oui, et tu peux simplifier un tout petit peu pour obtenir un truc que tu devrais savoir interpréter géométriquement.
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 16:13
par morgan88700 » 21 Jan 2010, 16:13
Donc en simplifiant J'obtient
||-MG||=||MI||
Mais est ce que MI c'est la médiatrice du segment AB ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Jan 2010, 16:20
par Doraki » 21 Jan 2010, 16:20
M serait sur la médiatrice de [AB] si t'avais (en distances) que MA = MB.
Là t'as pas que MA = MB ; t'as que MI = MG.
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 16:26
par morgan88700 » 21 Jan 2010, 16:26
Ouai -MG=MI donc MI+MG=0 donc M c'est le milieu de IG ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 16:45
par Dinozzo13 » 21 Jan 2010, 16:45
morgan88700 a écrit:||-MG||=||MI||
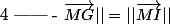
équivaut à
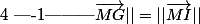
ce qui équivaut à
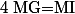
donc l'ensemble est ...
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 16:50
par morgan88700 » 21 Jan 2010, 16:50
Un cercle de centre M ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 16:51
par Dinozzo13 » 21 Jan 2010, 16:51
C'est l'ensemble des points équidistants de G et I donc la médiatrice du segment [IG]
-
morgan88700
- Messages: 9
- Enregistré le: 19 Nov 2008, 16:14
-
 par morgan88700 » 21 Jan 2010, 16:53
par morgan88700 » 21 Jan 2010, 16:53
Merci bcp pour cette aide très précieuse ! Bonne fin d'après midi !
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Jan 2010, 16:54
par Dinozzo13 » 21 Jan 2010, 16:54
A toi aussi, n'hésite pas à revenir :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
