Barycentre

[Aerialls]

Bonjour
J'ai un problème sur le barycentre (si si ca existe :p)

ABC est un triangle, la bissectrice intérieure de l'angle intérieure de l'angle BAC coupe [BC] en U

On admet que

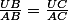
--> En déduire que U est barycentre de {(B;AC);(C;AB)}

Et je ne vois pas du tout comment faire :triste:

Merci de votre aide

[Elsa_toup]

Bonjour,

Je ne comprends pas bien cette notation :

U est barycentre de {(B;AC);(C;AB)}

Peux-tu me l'expliquer ?

[johnjohnjohn]

Bonjour,

Je ne comprends pas bien cette notation :

Peux-tu me l'expliquer ?

Pour ma part je n'osais pas poser la question. Peut être que ça veut dire que les longeurs AC et AB sont respectivement les coefficients de pondération des points B et C. Je n'oserais pas l'affirmer pour autant ....

[Elsa_toup]

Oui, je pense que tu as raison, johnjohnjohn.
Si c'est le cas, c'est assez simple:

D'après l'égalité, on a que: UC = UB * (AC/AB)
Or U, C et B sont alignés, donc on peut introduire une notion de vecteur dans l'égalité.
On a :
soit

Donc

D'où le résultat.

[johnjohnjohn]

Oui, je pense que tu as raison, johnjohnjohn.
Si c'est le cas, c'est assez simple:

D'après l'égalité, on a que: UC = UB * (AC/AB)
Or U, C et B sont alignés, donc on peut introduire une notion de vecteur dans l'égalité.
On a :
soit

Donc

D'où le résultat.

Pour ma part j'avais perdu de vue que U,C,B étaient alignés ...

C'est bouclé.