Barycentre

par **lucie78** » 23 Sep 2006, 12:48

bonjour!j'ai un problème avec une question d'un exercice je comprends rien du tout je vois pas comment on peut faire... :triste: est-ce que quelqu'un pourrait m'aider svp??merci!!

ps: toutes les longueurs que j'écris telles que AC,AB...etc sont en fait tous des vecteurs mais c'est que je sais pas comment on met la flèche au dessus...dsl)

on a CJ=2/5CB et AK=3AC,
puis moi j'ai trouvé A barycentre de (B;1) et (I;1)
C barycentre de (J;1) et (B;-2/5)
K barycentre de (A;2) et (C;-3)

question: démontrer que I,J,K alignés

par **zebdebda** » 23 Sep 2006, 13:02

Comment est défini le point I dans l'énoncé ?

Sinon pour répondre à la question tu dois montrer que IJ et IK sont colinéaires, ou que l'un des 3 points est un barycentre des 2 autres

par **lucie78** » 23 Sep 2006, 13:12

on a rien d'autre sur I...
j'ai essayé la méthode pour démontrer que l'un est le barycentre des deux autres mais le problème c'est que je ne sais pas d'ou partir et je n'arrive pas a débuter.est-ce que tu pourrais m'indiquer comment faire et après je me débrouillerai parce que la je vois vraiement pas quoi faire de tout ca!merci

par **lucie78** » 23 Sep 2006, 13:13

ah si oups pardon! I est le milieu de [AB]

par **zebdebda** » 23 Sep 2006, 13:14

Tu dis :

lucie78 a écrit: j'ai trouvé A barycentre de (B;1) et (I;1)

Tu dois forcément avoir une information sur I pour avoir trouvé ça...?

par **zebdebda** » 23 Sep 2006, 13:16

D'accord !
et les questions précédentes c'était demandé quoi précisément ?

car je pense qu'il aurait été plus logique d'exprimer I, J et K comme barycentre des autres points

par **lucie78** » 23 Sep 2006, 13:19

bah il fallait exprimer A barycentre de B et I, C barycentre de J et B et K barycentre de A et C

par **c pi** » 23 Sep 2006, 13:24

Pour montrer que les points I, J et K sont alignés
il suffit de montrer qu'il existe un nombre

tel que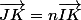

,
cette égalité traduisant la colinéarité des deux vecteurs,
une autre manière de dire que les deux droites (IK) et (JK) passant par K ont même direction.

A l'aide des coordonnées des points I, J et K
tu peux calculer les composantes des vecteurs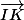

et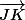

,
puis montrer qu'il existe un tel nombre

.

Si tu veux écrire les vecteurs avec les notations habituelles, tu peux utiliser les balises TEX.
Ainsi pour afficher

, tu tapes [TEX ]\vec{AB}[/TEX ] sans les espaces entre TEX et ].

par **zebdebda** » 23 Sep 2006, 13:25

D'accord

Alors tu dois savoir que tu peux "combiner" des barycentres

c'est-à-dire renplacer un point pondéré par les points dont il est barycentre, à condition que la somme des poids soient le poid de départ

Lourd à avaler ! je te donne un exemple.

Si M est le barycentre de (R,3) et de (S,1)
et N est le barycentre de (M,4) et (T,7)
alors N est le barycentre de (R,3) (S,1) et (T,7)

car on a bien 3+1=4

Avec ces combinaisaons tu devrais réussir à démontrer que K est un barycentre de I et J

par **lucie78** » 23 Sep 2006, 13:29

ah oui ok je comprends mieux!oui ca je sais faire mais je n'y avais pas pensé!merci beaucoup!

par **zebdebda** » 23 Sep 2006, 13:29

de rien ! il y a encore une astuce plus tard... si tu bloques n'hésite pas à redemander

par **lucie78** » 23 Sep 2006, 13:37

oui en fait j'ai réussi a démontrer que K barycentre de (I;1) mais j'arrive pas à démontrer qu'il est aussi barycentre de J... :briques:

par **zebdebda** » 23 Sep 2006, 13:44

que de (I,1) ?? c'est impossible (barycentre d1 seul point ça voudrait dire K=I)

tu as sans doute utilisé :
A barycentre de (B;1) et (I;1)
et K barycentre de (A;2) et (C;-3)

par **lucie78** » 23 Sep 2006, 13:49

euh oui c'est ce que j'ai fait... mais en fait j'ai trouvé K barycentre de (B;1) (I;1) et (C;-3) mais j'arrive pas a trouver J...

par **zebdebda** » 23 Sep 2006, 13:50

lucie78 a écrit:puis moi j'ai trouvé A barycentre de (B;1) et (I;1)

il y a une erreur ici : I est le milieu de [AB] : il y a des erreurs dans les poids de B et I

tu n'arriveras pas au résultat avec cette erreur

par **lucie78** » 23 Sep 2006, 13:55

ah bon? parce que en fait moi j'ai dis que AI=1/2AB donc pour moi I est affecté du coefficient 1 et B aussi... aie,je vois pas ou est mon erreur :marteau:

par **zebdebda** » 23 Sep 2006, 14:00

AI=1/2AB donc

donc A est barycentre de ...

par **lucie78** » 23 Sep 2006, 14:01

ah oui donc A barycentre de (I,1) et (B,-1/2)

par **zebdebda** » 23 Sep 2006, 14:03

maintenant c'est juste.

Je te rappelle la deuxième astuce dont tu vas avoir besoin.

Si M est barycentre de (R,r) et (S,s)
alors pour n'importe quel réel k non nul, M est barycentre de (R,kr) et (S,ks)

par **lucie78** » 23 Sep 2006, 14:05

oui ca j'y ai pensé je l'ai utilisé!merci beaucoup! :happy2:

Barycentre

barycentre

Qui est en ligne