Bonjour, j'ai un exercice de maths sur les barycentre le voici:
Soit ABCD un carré de centre 0||MB-MC+MD||=||MA-MB-MD|| il s'agit de vecteurs
1- Prouver que les points B et D appartiennent à l'ensemble (F)
J'ai d'abord trouver que le barycentre de A, B, C et D était O.
Puis O est le milieu de [DB] donc ||MD+MB||+||2MO|| il s'agit de vecteurs.
Donc B et D appartient à F.
2-Le point A appartient-il à F ? justifiez
J'ai fait la même chose que la question précédente.
3- Montrer que A est la barycentre du système (B,1) (C,-1) (D,1)
Donc on veut que MB-MC+MD=MA il s'agit de vecteurs
Je calcule G barycentre de ce système et je trouve BG=CD il s'agit de vecteur
4-Quel est le barycentre du système (A,1) (B,-1) (D,-1)
Je prend M=A donc AG=BA+DA (vecteur) donc le barycentre et la symétrie du point C par rapport au point A
5-Déduire des questions précédentes la nature de l'ensemble (F). Tracez (F)
Je n'arrive pas à répondre à cette question.
Merci d'avoir pris le temps de lire cette exercice, je voudrais savoir si mes réponses sont juste et ce que je pourrais améliorer
Barycentre
5 messages
- Page 1 sur 1
1- Prouver que les points B et D appartiennent à l'ensemble (F)
Ok
2-Le point A appartient-il à F ? justifiez
Euh A n'appartient pas à F si je ne m'abuse
3- Montrer que A est la barycentre du système (B,1) (C,-1) (D,1)
G = bar (O,2) (C,-1)

(solution alternative)
4-Quel est le barycentre du système (A,1) (B,-1) (D,-1)
Soit G ce barycentre. G = bar (A,1) (O,-2).

Donc ce serait plutôt C !
5-Déduire des questions précédentes la nature de l'ensemble (F). Tracez (F)
Pour ça il faut utiliser la propriété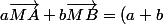 \vec{MG})
Ok
2-Le point A appartient-il à F ? justifiez
Euh A n'appartient pas à F si je ne m'abuse
3- Montrer que A est la barycentre du système (B,1) (C,-1) (D,1)
G = bar (O,2) (C,-1)
(solution alternative)
4-Quel est le barycentre du système (A,1) (B,-1) (D,-1)
Soit G ce barycentre. G = bar (A,1) (O,-2).
Donc ce serait plutôt C !
5-Déduire des questions précédentes la nature de l'ensemble (F). Tracez (F)
Pour ça il faut utiliser la propriété
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
