Barycentre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Vaanilly
- Membre Naturel
- Messages: 37
- Enregistré le: 17 Aoû 2010, 22:39
-
 par Vaanilly » 12 Jan 2011, 22:20
par Vaanilly » 12 Jan 2011, 22:20
Bonsoir ,
Voici un exercice sur lequels j'aurais besoin d'être guider car je n'y arrive pas .
Le voici ( chaque somme de vecteurs et compris entre deux barres exprimant " la distance " que je ne retrouve pas sur laTex. :-s
[AB] est un segment de longueur 10 cm .
Déterminer et construire l'ensemble des points M du plan tels que :
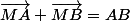
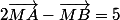
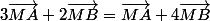
Je pensais trouver une relation me donnant qu'un certain vecteur est égal à x* un autre vecteur et ainsi trace le rayon correspondant à la longeur de ce vecteur mais cela reste très confus et je ne réussi à trouver les calculs pour en arriver à ce résultat .
Merci d'avance
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Jan 2011, 22:25
par Arnaud-29-31 » 12 Jan 2011, 22:25
Salut,
Tu dois introduire dans chaque relation vectorielle un barycentre bien choisi ...
Tu penses auquel déjà pour la 1ère ?
Par contre tu aurais pas oublié décrire les barres indiquant la norme ?
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 12 Jan 2011, 22:26
par Mortelune » 12 Jan 2011, 22:26
Bonsoir, posons M=(x,y), A=(a1,a2) et B=(b1,b2).
Alors on est capable d'exprimer les différents vecteurs.
Comme tu as des égalités sur des normes ça va te donner des équations en x et y à résoudre et tu pourras trouver des équations de cercles par exemple.
-
Vaanilly
- Membre Naturel
- Messages: 37
- Enregistré le: 17 Aoû 2010, 22:39
-
 par Vaanilly » 12 Jan 2011, 22:30
par Vaanilly » 12 Jan 2011, 22:30
Arnaud-29-31 a écrit:Salut,
Tu dois introduire dans chaque relation vectorielle un barycentre bien choisi ...
Tu penses auquel déjà pour la 1ère ?
Par contre tu aurais pas oublié décrire les barres indiquant la norme ?
Si désolé mais je ne l'ai ai pas trouvé sur laTex :/
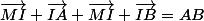
Jusque là ça va ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Jan 2011, 22:41
par Arnaud-29-31 » 12 Jan 2011, 22:41
Oui à condition de me dire ce qu'est I ... ca serait beau si

0 ...
-
Vaanilly
- Membre Naturel
- Messages: 37
- Enregistré le: 17 Aoû 2010, 22:39
-
 par Vaanilly » 12 Jan 2011, 22:50
par Vaanilly » 12 Jan 2011, 22:50
Arnaud-29-31 a écrit:Oui à condition de me dire ce qu'est I ... ca serait beau si

0 ...
Je suis vraiment perdu avec les vecteurs :triste: .
I serait donc le barycentre de (A;1) (B,1) ? ..
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 13 Jan 2011, 16:40
par Arnaud-29-31 » 13 Jan 2011, 16:40
Oui ... on peux aussi l'appeler milieu de [AB].
De manière générale, lorsque tu as

tu introduis G le barycentre de (A,a);(B,b) et tu as ainsi
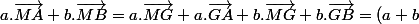.\vec{MG})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
