Barycentre milieu d'un segment -> pas dur ^^

[Mobster]

Bonjoir :)
Alors il faut que je détermine en gros que C appartient au segment [AB] sachant que j'ai démontré que C est le barycentre de {(A,1),(B,3)}.
Y'a-t-il un calcul pour montrer qu'il est bien sur le segment et pas sur la droite (sans le segment) ? Car sinon je vais devoir le dire en me débrouillant à l'à-peu-près \o/

[Arnaud-29-31]

Bonsoir,

En effet, c'est pas dur ^^

[Ben314]

Salut,
Tout dépend de la définition que l'on prend d'un "segment".

Certains bouquins prennent comme définition du segment [AB] l'ensemble de barycentres de A et B affectés e coeffs. positifs.
Dans ce cas, y'a rien à dire, ton point appartient au segment... par définition.

Si tu veut quand même faire un "morceaux de preuve", je te conseillerais de montrer que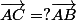 où ? est un réel entre 0 et 1 et de dire que ça "prouve" que C appartient au segment.

[Arnaud-29-31]

Bon sans rire, puisque tu sais que C = bary[(A,1);(B,3)], tu as tu introduis le point A ou B (relation de Chasles),
par exemple A :
et finalement et comme 3/4 est inférieur à 1 ...

[Mobster]

xD je me sens honteuuuux ! Merci beaucoup à tous x)

[Mobster]

Hum je bloque à la question juste après --',
Alors j'ai K=bary{(A,1)(B,1)(C,1)(D,1)} et H=bary{(A,1)(C,2)(D1)}
et il faut que je détermine l'ensemble (E1) des points M de l'espace tels que :
||MA + MB + MC + MD|| = ||MA + 2MC + MD||.
J'ai introduit les barycentres dans cette équation, mais je ne vois pas comment continuer..

[Mobster]

J'ai trouve, y'avait juste une formule que j'avais plus en tête. On tombe sur MK = MH, c'est bien ça ?

[Arnaud-29-31]

Et oui, on tombe bien sur ça ...