Bonjour !
Enoncé : ABC est un triange. On considère le barycentre de A' de (B,2) et (C, -3), le barycentre de B' de (A,5) et (C,-3) ainsi que le barycentre C' de (A,5) et (B,2).
Démontrer que les droites (AA'), (CC') et (BB') sont concourantes.
Ce que j'ai fait :
J'ai calculé :
-le barycentre A', j'ai trouvé :
(On parle ici de vecteurs)
BA' = 3BC
-le barycentre B', j'ai trouvé :
(On parle ici de vecteurs)
AB' = 3/2 AC
-le barycentre C', j'ai trouvé :
(On parle ici de vecteurs)
CA' = 2/7 BA
Pour la suite je suis perdu... je n'arrive même pas à construire le triangle... :help:
Barycentre dans un triangle
9 messages
- Page 1 sur 1
Bon, déjà, à mon avis il y a deux erreurs dans ton énoncé :
i) Le point C', c'est le barycentre C' de (A,5) et (B ,2).
ii) Ce qu'il faut montrer c'est que les trois droites (AA'), (BB') et (CC') sont concourantes.
ce qui explique en grande partie que personne ne te réponde...
Ensuite, si tu veut absolument passer par les vecteurs (ce qui à mon avis n'est pas la meilleure solution : on peut trés bien s'en sortir en n'utilisant que des baricentres), il faut que tu montre qu'il existe un point M qui :
- soit situé sur la droite (AA') donc tel que pour un certain réel
pour un certain réel 
- soit situé sur la droite (BB') donc tel que pour un certain réel
pour un certain réel 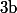
- soit situé sur la droite (CC') donc tel que pour un certain réel
pour un certain réel 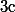
En utilisant Chasle, regroupe ces égalités en égalités ne parlant que de a,b,c et pas de M...
i) Le point C', c'est le barycentre C' de (A,5) et (B ,2).
ii) Ce qu'il faut montrer c'est que les trois droites (AA'), (BB') et (CC') sont concourantes.
ce qui explique en grande partie que personne ne te réponde...
Ensuite, si tu veut absolument passer par les vecteurs (ce qui à mon avis n'est pas la meilleure solution : on peut trés bien s'en sortir en n'utilisant que des baricentres), il faut que tu montre qu'il existe un point M qui :
- soit situé sur la droite (AA') donc tel que
- soit situé sur la droite (BB') donc tel que
- soit situé sur la droite (CC') donc tel que
En utilisant Chasle, regroupe ces égalités en égalités ne parlant que de a,b,c et pas de M...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Bon, déjà, à mon avis il y a deux erreurs dans ton énoncé :
i) Le point C', c'est le barycentre C' de (A,5) et (B ,2).
ii) Ce qu'il faut montrer c'est que les trois droites (AA'), (BB') et (CC') sont concourantes.
ce qui explique en grande partie que personne ne te réponde...
Ensuite, si tu veut absolument passer par les vecteurs (ce qui à mon avis n'est pas la meilleure solution : on peut trés bien s'en sortir en n'utilisant que des baricentres), il faut que tu montre qu'il existe un point M qui :
- soit situé sur la droite (AA') donc tel quepour un certain réel
- soit situé sur la droite (BB') donc tel quepour un certain réel
- soit situé sur la droite (CC') donc tel quepour un certain réel
En utilisant Chasle, regroupe ces égalités en égalités ne parlant que de a,b,c et pas de M...
Trouver une erreur dans un énoncé est une chose, mais le corriger en est une autre Oo Chapeaux ! J'ai corrigé
Merci beaucoup pour ta réponse
Mais je ne le comprend pas :mur:
Edit : J'ai réussis à l'appliquer uniquement pour ce cas :
G est barycentre de (A,5),(C,-3) (B,2)
donc aussi de (B,2) (B,2)
D'ou : G appartient (BB').
Je te donne quand même la fin de la "méthode vectorielle" (j'aime pas un truc qui reste en plan...)
L'objectif est de TOUT exprimer en fonction de A,B,C et même plus précisément uniquement en fonction des vecteurs AB et AC.
La deuxième relation peut s'écrire) .
.
Or tu as montré que et que
et que 
donc et
et  et la relation
et la relation ) peut s'écrire :
peut s'écrire :
=\vec{BA}+a\left( \vec{AB}+3\vec{BC}\right)) ou encore :
ou encore :
\vec{AB}-\frac{3b}{2}\vec{AC}+3a\vec{BC}= (a+b-1)\vec{AB}-\frac{3b}{2}\vec{AC}+3a\left(\vec{BA}+\vec{AC} \right) =(-2a+b-1)\vec{AB}+\left(3a-\frac{3b}{2}\right)\vec{AC})
Sauf que, comme A,B et C sont non alignés, cette relation signifie que ce qui permet de trouver 'a' et 'b'.
ce qui permet de trouver 'a' et 'b'.
Il n'y a plus qu'à (!!!) faire la même chose avec la troisième relation et regarder si on trouve bien le même 'b'
Concernant la "bonne" méthode (avec les barycentre), il te suffit effectivement de considérer le barycentre G=bar( (A,5) ; (B,2) ; (C,-3) ).
L'associativité des barycentre te dit que tu peut remplacer deux (ou plus) des points pondérés dans un barycentre par le barycentre de ces deux (ou plus) point qui se retrouve avec un "poid" égal à le somme des poids des points qu'il remplace.
Par exemple, vu que C'=bar( (A,5) ; (B,2) ), dans le barycentre bar( (A,5) ; (B,2) ; (C,-3) ), tu peut remplacer (A,5) ; (B,2) par (A',5+2)...
L'objectif est de TOUT exprimer en fonction de A,B,C et même plus précisément uniquement en fonction des vecteurs AB et AC.
La deuxième relation peut s'écrire
Or tu as montré que
donc
Sauf que, comme A,B et C sont non alignés, cette relation signifie que
Il n'y a plus qu'à (!!!) faire la même chose avec la troisième relation et regarder si on trouve bien le même 'b'
Concernant la "bonne" méthode (avec les barycentre), il te suffit effectivement de considérer le barycentre G=bar( (A,5) ; (B,2) ; (C,-3) ).
L'associativité des barycentre te dit que tu peut remplacer deux (ou plus) des points pondérés dans un barycentre par le barycentre de ces deux (ou plus) point qui se retrouve avec un "poid" égal à le somme des poids des points qu'il remplace.
Par exemple, vu que C'=bar( (A,5) ; (B,2) ), dans le barycentre bar( (A,5) ; (B,2) ; (C,-3) ), tu peut remplacer (A,5) ; (B,2) par (A',5+2)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:
Concernant la "bonne" méthode (avec les barycentre), il te suffit effectivement de considérer le barycentre G=bar( (A,5) ; (B,2) ; (C,-3) ).
L'associativité des barycentre te dit que tu peut remplacer deux (ou plus) des points pondérés dans un barycentre par le barycentre de ces deux (ou plus) point qui se retrouve avec un "poid" égal à le somme des poids des points qu'il remplace.
Par exemple, vu que C'=bar( (A,5) ; (B,2) ), dans le barycentre bar( (A,5) ; (B,2) ; (C,-3) ), tu peut remplacer (A,5) ; (B,2) par (A',5+2)...
C'=bar ( (A,5) ; (B,2) ), dans le barycentre bar ( (A,5) ; (B,2) ; (C,-3) )
Donc C'=bar ( (A,7) ; (C,-3) )
B'=bar ( (A,5) ; (C,-3) ), dans le barycentre bar ( (A,5) ; (B,2) ; (C,-3) )
Donc B'=bar ( (A,2) ; (B,2) )
A'=bar ( (B,2) ; (C,-3), dans le barycentre bar ( (A,5) ; (B,2) ; (C,-3) )
Donc B'=bar ( (B,1) ; (A,5) )
C'est bien ça ?
leszeus a écrit:C'=bar ( (A,5) ; (B,2) ), dans le barycentre bar ( (A,5) ; (B,2) ; (C,-3) )
Donc C'=bar ( (A,7) ; (C,-3) )
B'=bar ( (A,5) ; (C,-3) ), dans le barycentre bar ( (A,5) ; (B,2) ; (C,-3) )
Donc B'=bar ( (A,2) ; (B,2) )
A'=bar ( (B,2) ; (C,-3), dans le barycentre bar ( (A,5) ; (B,2) ; (C,-3) )
Donc B'=bar ( (B,1) ; (A,5) )
C'est bien ça ?
Ben non, c'est pas du tout ça...
Dans le barycentre G=bar ( (A,5) ; (B,2) ; (C,-3) ) , comme C'=bar ( (A,5) ; (B,2) ), on peut "remplacer" (A,5) ; (B,2) par (C',5+2) et on obtient G=bar ( (C',7) ; (C,-3) )
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Ben non, c'est pas du tout ça...
Dans le barycentre G=bar ( (A,5) ; (B,2) ; (C,-3) ) , comme C'=bar ( (A,5) ; (B,2) ), on peut "remplacer" (A,5) ; (B,2) par (C',5+2) et on obtient G=bar ( (C',7) ; (C,-3) )
Dans le barycentre G=bar ( (A,5) ; (B,2) ; (C,-3) ) on a :
C'=bar ( (A,5) ; (B,2) ),
donc G=bar ( (C',7) ; (C,-3) )
B' = ( (A,5) ; (C,-3) ),
donc G=bar ( (B', 2) ; (B,2) )
A' = ( (B,2) ; (C,-3) ),
donc G=bar ( (A',-1) ; (A,5) )
(AA'), (BB'), (CC') sont donc concourantes en G.
A mon avis c'est ça :doh:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
