[1èreS] Barycentre et coordonnées

par **Gtadore** » 31 Oct 2009, 12:20

Bonjour à tous :we:
J'ai un DM sur les barycentres à faire, pas trop compliqué... jusqu'à cet exercice !

Dans un repère orthonormé (O;i;j;k) j'ai les coordonnées de 4 points : A(3;8;0), B(4;10;-2), C(-2;-2;-12) et G(2;6;3)
On me demande s'il existe des réels a, b et c tel que G barycentre de (A;a), (B;b) et (C;c)

La réponse doit surement être oui vu que la question suivante demande de déterminer ces réels :hein:
Et je ne vois absolument pas comment faire cet exo, j'ai essayer de calculer les coordonnées des vecteurs AG BG et CG mais ça n'a rien donner...

Donc voila, merci de votre aide ^^

par **Timothé Lefebvre** » 31 Oct 2009, 12:22

Bonjour :)

Utilise la définition vectorielle du barycentre.

par **Gtadore** » 31 Oct 2009, 17:13

Celle qui dit que aGA+bGB+cGC = 0 ?
Mais après si j'ai les coordonnées de GA GB et GC, je suis obligé d'y faire de tête... :hein:

par **Dinozzo13** » 31 Oct 2009, 17:38

Premièrement tu dois définir quand est-ce que G existe suivant a,b et c.
Ensuite, cacule les coordonnées de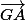

,

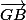et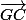

.
Or d'après la définition, G est le barycentre de (A,a),(B,b) et (C,c) si et seulement si

. Or tu cherche des coordonnées dans l'espace donc, tu remplace sous forme d'un système de 3 équations à trois inconnues l'expression du barycentre G.

par **Gtadore** » 01 Nov 2009, 15:14

Donc je trouve

(1;2;-3),

(2;4;-5) et

(-4;-8;-15)

Après je fais

(a;2a;-3a),

(2b;4b;-5b) et

(-4c;-8c;-15c) ?

Donc après les 3 équations ça seraient : a+2b-4c=0 ; 2a+4b-8c=0 et -3a-5b-15c=0 ?

Et si j'ai juste bah...j'ai plus qu'à apprendre à faire des équations à 3 inconnues mdr

par **Dinozzo13** » 02 Nov 2009, 00:38

:++: tout va bien, il ne te reste plus qu'à résoudre :

par **Gtadore** » 02 Nov 2009, 09:52

Oula on a jamais fait ca mdr
Bon en essayant d'y faire tout seul je trouve...bah je trouve pas enfaite :triste: Ca serait pas à cause des 0 que je trouve pas :hum:

par **Dinozzo13** » 02 Nov 2009, 12:13

Je vais t'aider, Soit

la 1re équation, et

,

les deux autres, effectue les opérations suivantes :

Une fois que tu as calculé ça, résous le système que tu as calculé :

ce système a deux inconnues b et c car les calculs précédents ont pour but de supprimer les termes en a dans les deux dernières équations.
Ensuite, tu remplace b et c dans (E), tu en déduis a ^^.

par **Gtadore** » 02 Nov 2009, 17:42

Je suis pas très vaillant là donc je vais pas le faire maintenant mais ça à pas l'air trop dur ^^
Mais pour (E1)-2(E), tout les termes s'annulent :hein:

par **Dinozzo13** » 02 Nov 2009, 21:11

c'est possible, je ne sais pas, je ne l'ai pas fait.

par **benekire2** » 02 Nov 2009, 21:14

Gtadore a écrit:Je suis pas très vaillant là donc je vais pas le faire maintenant mais ça à pas l'air trop dur ^^
Mais pour (E1)-2(E), tout les termes s'annulent :hein:

Effectivement.
Tu n'as qu'a le faire par substitution au pire... comme avec les systèmes d'équations a deux inconnues...

[1èreS] Barycentre et coordonnées

[1èreS] Barycentre et coordonnées

Qui est en ligne