(barycentre) Barycentres partiels - Intersection de droites

[bac2012s]

Bonjour je n'arrive pas à comprendre au 3)
http://xmaths.free.fr/1S/exos/exercice.php?nomexo=1SbaryexC4

pourquoi il conclue que : le point est sur la droite, je comprend le consept mais pas la finalité...
solution : http://xmaths.free.fr/corrections/z7755qr7c2.pdf

Cordialement

[mathelot]

bah vi, si K est un point de la droite (AC), K est barycentre de A et C

théorème: une variété linéaire affine (point,droite,plan,hyperplan) de dimension est aussi l'ensemble des barycentres de de ses points , affinement indépendants

[didou31]

Tu as vu que tu peux remplacer la définition du barycentre G : (A;-1) (B;2) (C;3) par G barycentre (I;-1+2) (C,3). I étant un barycentre partiel. Ce tour de passe-passe se démontre aisément dans le cas général. (Ca pourrait être le sujet d'un exercice.)
Cela signifie que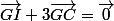 . C'est une relation de vecteurs colinéaires. Ce qui signifie que G, I et C sont alignés. Et ça démontre la première partie de la question 3).

Même méthode pour montrer que G appartient à (AJ).

[bac2012s]

Tu as vu que tu peux remplacer la définition du barycentre G : (A;-1) (B;2) (C;3) par G barycentre (I;-1+2) (C,3). I étant un barycentre partiel. Ce tour de passe-passe se démontre aisément dans le cas général. (Ca pourrait être le sujet d'un exercice.)
Cela signifie que . C'est une relation de vecteurs colinéaires. Ce qui signifie que G, I et C sont alignés. Et ça démontre la première partie de la question 3).

Même méthode pour montrer que G appartient à (AJ).

oui en gros k= -1 (cela dépends dans quel sens on a mis le barycentre dans le 1)
IA - 2IB => -AI +2BI...

ah oui j'ai saisit ds la determination de G sur la droite IC que :
IG = 3/4 CI
CG = 1/4 CI
et avec un compas on voit bien que que cela tombe sur la droite CI et on peut créer le point G