Barycentre avec parametre - ensemble de points

[Dinozzo13]

Bonsoir, ^^, j'ai un petit exercice de révision sur le barycentre mais je ne suis pas sûr de ce que j'ai fait pour la dernière question, j'aimerais donc savoir si il y a des erreurs, merci d'avance.

On considère un triangle et un réel.
1°) Pour quelle(s) valeur(s) de le barycentre des points pondérés existe-t-il ?

Ce barycentre est défini si et seulement si .
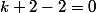
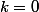
Je résous , donc est défini si et seulement si .

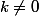
2°) Lorsque G_k existe, démontrer que .

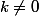
Pour tout , est le barycentre de , donc pour tout :

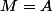
Si alors
d'où .

3°) Justifier que le quadrilatère est un parallélogramme.

si k=2 alors donc est un parallélogramme.

4°) Déterminer l'ensemble des points lorsque décrit l'intervalle .

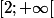
Lorsque k décrit cet intervalle j'ai mis que :
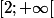
donc que , or donc . Par conséquent, lorsque décrit , l'ensemble des points est le segment privé du point .

Voilà, merci encore :ptdr: :ptdr: :ptdr: :ptdr: .

[bombastus]

Salut,

effectivement la rédaction de la dernière question laisse à désirer...

bon, à la limite si tu trouve une théorie qui permet les inégalité entre vecteur, pourquoi pas, mais malheureusement pour toi, à ma connaissance un tel outil n'existe pas!! :marteau:

Maintenant ce que tu peux comparer, c'est les normes en profitant du fait que les vecteurs sont colinéaires...

[Dinozzo13]

^^ ah, ça n'existe pas les inegalités de vecteurs ??? dans ce cas oui, j'utiliserai des normes à la place. Est-ce que mon idée de limite est bonne ou on peut l'exprimer autrement ???

[bombastus]

Oui, je pense que l'idée est bonne en précisant que la fonction f(x) = a*2/x est monotone sur l'intervalle dans lequel tu travailles pour être rigoureux et justifier les inégalités.

[Dinozzo13]

ok, je reverrai tout ça demain matin ^^