Salut à tous, de retour avec un autre sujet du baccalauréat C de l'académie d'Aix-Marseille, cette fois celui de 1977.
Dans l'exo 1 donné ci-dessous :

La question 1) est une question élémentaire d'arithmétique.
En effet, si
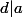
et
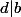
alors
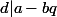
donc si

est un diviseur commun à

et

c'est aussi un diviseur commun à

et de
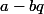
.
Réciproquement, si
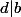
et
)
alors
) = a)
donc

est aussi un diviseur commun à

et à

.
Conclusion : l'ensemble des diviseurs de

et

est l'ensemble des diviseurs de

et de
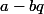
. En particulier
)
.
Cependant, n'y a-t-il pas une erreur dans la question 2) ?
On essaye d'appliquer le résultat de la question 1)
Effectuons la division euclidienne de
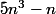
par
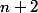
. On trouve que
 (5n^2 + 10n - 19) -38)
On a alors d'après 1) :
 \wedge 38)
et non
)
je me trompe ?
Pour la 3) on a que
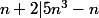
ssi
 \wedge (n+2) = (n+2) \wedge 38)
c'est à dire, puisque
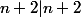
, ssi
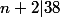
.
L'ensemble des diviseurs de
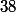
dans

étant
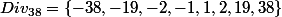
on en déduit que
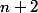
divise
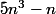
ssi
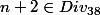
c'est à dire
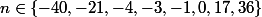
.
Pour la 4) je pense qu'il y a plusieurs manières de faire mais on peut résoudre "à la main" comme ceci : on sait que l'ensemble des valeurs de
 \wedge (n+2))
est l'ensemble des valeurs de
 \wedge 38)
c'est à dire
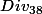
. Si on veut
 \wedge 38 = 19)
alors il faut et il suffit que
)
mais que
)
donc
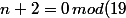)
mais
)
. On en déduit immédiatement que

et
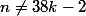
,
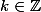
donc
 - 2 = 38k + 17)
,
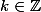
.

