Axiome de Peano

[Achtax]

L'énoncé complet :

Soit A une partie non vide de N contenant 0.

1. A quelle condition sur A\ a-t-on A=N ?

2.Supposons cela non vérifié
Soit n le plus petit élément de A\
Démontrer n-1 appartient à A

3. En déduire A=N

Tout va bien jusqu'à la 3

[leon1789]

A est la partie de N qui contient tous les successifs.
B est la partie complémentaire pour former N.

B contient alors un entier k.
et alors il existe des entiers k-1,k-2,..., k-k=0

là, je ne suis pas d'accord : comment savoir qu'il existe i tel que k-i = 0 ? Il faut une définition des entiers qui prouve cela.
Si ça se trouve k-1 n'est pas entier car k n'est le successeur de personne...

[leon1789]

L'énoncé complet :

Soit A une partie non vide de N contenant 0.

1. A quelle condition sur A a-t-on A=N ?

Tu as répondu quoi à cette question ?

[Achtax]

A\ doit logiquement être égal à ensemble vide non ?

[beagle]

là, je ne suis pas d'accord : comment savoir qu'il existe i tel que k-i = 0 ?

ben parce que k est un entier,
donc c'est du 1 et du 1 et du 1 et du 1 et du 1, ...
donc moi j'enlève les 1 et les 1 et les 1 jusqu'à zéro.

Bon j'ai jamais fait péano, mème si j'aime bien ce que tu fais avec (c'est pas la première fois que je te vois jouer avec péano).
Pour moi, perso j'ai fait mathématique moderne, uniquement la théorie des ensembles.
donc j'imagine k comme une patate remplie de 1.
bon je me contente de peu aussi!

Si k est une patate de 1,
k-1 est la patate où on enlève un 1.

[leon1789]

A\ doit logiquement être égal à ensemble vide non ?

ok, si le complémentaire de A dans N est vide, alors A = N

Pour la question 2),
comment démontrer que n-1 est un entier ? C'est le même problème qu'avec beagle.

[beagle]

ok, si le complémentaire de A dans N est vide, alors A = N

Pour la question 2),
comment démontrer que n-1 est un entier ? C'est le même problème qu'avec beagle.

n est ensemble de 1
n-1 est l'ensemble de 1 qui a un élément de moins.

[Achtax]

moi je pensais que si n est un entier naturel pas égal à 0 alors il possède un successeur et un prédécesseur et si n est le plus petit élément de A\ alors le prédécesseur de n est contenu dans A or le prédécesseur de n est logiquement n-1

[leon1789]

ben parce que k est un entier,
donc c'est du 1 et du 1 et du 1 et du 1 et du 1, ...

Là, tu es en train de dire que tout entier non nul est le successeur d'un entier distinct.
Ce n'est pas dans les axiomes de Péano, mais cela peut peut-être suffire (en y ajoutant les 4 premiers axiomes de Péano) à définir les entiers.

Pour moi, perso j'ai fait mathématique moderne, uniquement la théorie des ensembles.
donc j'imagine k comme une patate remplie de 1.
bon je me contente de peu aussi!

Si k est une patate de 1,
k-1 est la patate où on enlève un 1.

Je comprends bien.
Le problème est que, pour démontrer des assertions de base, il faut faire les choses dans le bon ordre, sans même la charrue avant les boeufs, ni admettre le résultat de manière sous-entendu pour le démontrer ensuite. Tu comprends ce que je veux dire. Il est donc impératif de se fixer de bonnes règles du jeu.

[Achtax]

Pour démontrer que n-1 est un entier A\ ne contient pas 0 et contient n on a donc tous les élément de A et A\ qui appartiennent a N d'ou n et n-1 appartiennent à N

[leon1789]

moi je pensais que si n est un entier naturel pas égal à 0 alors il possède un successeur et un prédécesseur

Justement, "tout entier non nul possède un prédécesseur" n'est pas quelque chose d'anodin.
Par exemple, ce n'est pas dans les axiomes de Péano.

Donc maintenant, je comprends quelles sont les règles de ton jeu :
1/ 0 est un entier naturel.
2/ Tout entier naturel n a un unique successeur
3/ Aucun entier naturel n'a 0 pour successeur.
4/ Deux entiers naturels ayant même successeur sont égaux.
5/ Tout entier naturel non nul est le successeur d'un autre entier naturel

Avec ces cinq axiomes, il faut démontrer >

C'est bien ça ?

[Achtax]

Exactement =)

[leon1789]

Donc maintenant, je comprends quelles sont les règles de ton jeu :
1/ 0 est un entier naturel.
2/ Tout entier naturel n a un unique successeur
3/ Aucun entier naturel n'a 0 pour successeur.
4/ Deux entiers naturels ayant même successeur sont égaux.
5/ Tout entier naturel non nul est le successeur d'un autre entier naturel

hum, je crains que cela ne suffisent pas pour définir les entiers naturels.
Par exemple, R\{-1} vérifie ces 5 axiomes (la fonction successeur étant moralement x -> x+1)
et on pourrait appeler entier les éléments de R\{-1}...

[leon1789]

Donc maintenant, je comprends quelles sont les règles de ton jeu :
1/ 0 est un entier naturel.
2/ Tout entier naturel n a un unique successeur
3/ Aucun entier naturel n'a 0 pour successeur.
4/ Deux entiers naturels ayant même successeur sont égaux.
5/ Tout entier naturel non nul est le successeur d'un autre entier naturel

hum, je crains que cela ne suffisent pas pour définir correctement les entiers naturels.

Par exemple, vérifie ces 5 axiomes (la fonction successeur étant moralement x -> x+1)
et on pourrait appeler "entiers" les éléments de , ce qui ne convient évidemment pas pour nous.

[Achtax]

Je ne vois pas bien ou tu veux en venir enfaite ..
En effet pour moi le but de ce DM est de démontrer le 5eme axiome de péano à l'origine de la récurrence et non pas définir l'ensemble N.

[Achtax]

Apres si je suis ton raisonnement il suffirait d'ajouter :
Tout entier naturel n a un unique successeur noté n+1

[leon1789]

Je ne vois pas bien ou tu veux en venir enfaite ..
En effet pour moi le but de ce DM est de démontrer le 5eme axiome de péano à l'origine de la récurrence et non pas définir l'ensemble N.

Comme je disais plus haut, pour faire une preuve correcte, il faut partir d'axiomes pour en déduire des résultats.
Pour arriver à tes fins, il faut partir avec les bons axiomes, sinon c'est peine perdue !
Pour l'instant, on n'a pas encore une liste d'axiomes suffisante (des axiomes définissant les entiers naturels) pour espérer démontrer ce que tu veux sur l'ensemble des entiers naturels...
Comment démontrer des choses sur les entiers s'ils ne sont pas correctement définis ?

[leon1789]

Il y a différentes manières de définir les entiers : voir
https://fr.wikipedia.org/wiki/Axiomes_de_Peano
http://champagne.jacques.pagesperso-orange.fr/mapage3/chapitre-9-entiers-naturels-ensembles-finis.pdf
http://math.univ-lyon1.fr/~caldero/Blanchon-TIPE.pdf
Les unes démontrent les autres, mais il faut encore savoir d'où on part...

[Achtax]

Je partirai de la définition du second lien à mon avis car je ne peut décemment pas partir des axiomes de peano pour démontrer le 5ème axiomes de peano.

[leon1789]

ok.

Alors notons A un sous-ensemble de N tel que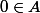 et

Notons A\ le complémentaire de A dans N

Supposons A\ est non vide : alors, par l'axiome 1, A\ admet un plus petit élément, noté p
On a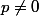 puisque .

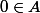Considérons l'ensemble des entiers de A strictement inférieur à p : B =
(on y a droit car N est totalement ordonné) . Alors B n'est pas vide car B contient 0 (0 est le plus petit élément de N)

Comme B est majoré (par p) et non vide alors, par l'axiome 2, B contient un plus grand élément, noté g.

En particulier g est dans A, donc g+1 est aussi dans A.
Or g+1 n'est pas dans B, et g+1 est le plus petit élément de
Donc , et comme g+1 n'est pas dans B, alors g+1=p.
Or p est un élément de A\ !! Contradiction.