Bonjour tout le monde, alors mon problème porte sur les barycentres...
Voici l'énoncé :
Soit un triangle ABC. On considère:
le barycentre I de (A;2)(C;1)
le barycentre J de (A:1)(B;2)
le barycentre K de (C;1)(B;-4)
1.Montrer que B est le barycentre de (K;3)(C;1)
2.En déduire le barycentre de (A;2)(K;3)(C;1)
3.Montrer que J est le milieu de [IK]
4.Soit L milieu de CI et M milieu de CK
a.Montrer que M est le bary. de (B;2)(C;1)
b.Montrer que ILMJ est un parallèlogramme
c.Et que O est le centre de ILMJ et de ABC
Mon problème commence au 4b...
HELP SVP! Merci d'avance
Avis aux amateurs de barycentre XD
6 messages
- Page 1 sur 1
O centre de IJLM,
F milieu de [BC].
Je suis un peu faineant, pour montrer que O centre de gravité de ABC, je vais juste montrer que O est situé au 2/3 de la mediane issue de A dans le triangle ABC.
(Comme tu le sais, le centre de gravité d'un triangle est situé au 2/3 de la mediane en partant du sommet.
En clair, Si G centre de gravité de ABC, ou F milieu de [BC]).
ou F milieu de [BC]).
O milieu de [JL] (car O centre de IJLM)
donc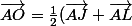)
Or (ca je te laisse peut-etre le montrer;)
(ca je te laisse peut-etre le montrer;)
donc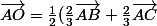= \frac 1 3 (\vec{AB}+\vec{AC})=\frac 1 3 (2\vec{AF}))
F milieu de [BC].
Je suis un peu faineant, pour montrer que O centre de gravité de ABC, je vais juste montrer que O est situé au 2/3 de la mediane issue de A dans le triangle ABC.
(Comme tu le sais, le centre de gravité d'un triangle est situé au 2/3 de la mediane en partant du sommet.
En clair, Si G centre de gravité de ABC,
O milieu de [JL] (car O centre de IJLM)
donc
Or
donc
Merci!!!!
Merci beaucoup pour tes réponses... Elles m'apportent une aide précieuse...
Comme ça tu as déja vu plus bizarre, un exemple ?
Bon eh bien encore un grand merci et à bientot, enfin, j'espère... XD
Bisous
Léa alias Lolaluna
Comme ça tu as déja vu plus bizarre, un exemple ?
Bon eh bien encore un grand merci et à bientot, enfin, j'espère... XD
Bisous
Léa alias Lolaluna
salut,
personnellement j'ai fait toutes tes questions en utilisant uniquement l'associativité, et je trouve ca plus pratique.
par exemple pour IJML parralélogramme, fallait juste montrer que M bar {(L,1) ; (J,1) ; (I,-1) }
avec l'associativité
et pour O tu montre que l'isobarycentre de I, J, M et L est l'isobarycentre de A, B et C avec l'associativité.
Bien sur il fallait jouer avec les coefficients en les multipliant (homogénéité du barycentre)
personnellement j'ai fait toutes tes questions en utilisant uniquement l'associativité, et je trouve ca plus pratique.
par exemple pour IJML parralélogramme, fallait juste montrer que M bar {(L,1) ; (J,1) ; (I,-1) }
avec l'associativité
et pour O tu montre que l'isobarycentre de I, J, M et L est l'isobarycentre de A, B et C avec l'associativité.
Bien sur il fallait jouer avec les coefficients en les multipliant (homogénéité du barycentre)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
