Bonjour je bloque sur cette exercice et je vous demande un peu d'aide s'il vous plait sur ça :
On se propose de comparer les entiers naturels:
A=13x8^100x(25)^50x(21)^15
B=11x4^100x10^100x(63)^7x(49)^4
1.Avec le signe de la différence
a)Décomposer A et B en produit de nombres premiers
b)Factoriser A-B
c)En déduire le signe de A-B
d)Comparer alors A et B
2.Avec un quotient
a)En utilisant la question 1.a), donner la fraction irréductible égale à A/B
b)Comparer alors A et B.
j'ai fait : A)
8 = 2^3 donc 8^100 = (23)^100 = 2^300
( 25 )^50= 5²= (25)^50 = 5^100
(21)^15 : 21 = 3 x 7 = (21)15 = 3^15 x 7^15
on obtient : A = 2^300 x 3^15 x 5^100 x 7^15 x 13
B) 4= 2² = 2^200
10^100 : 10 = (2*5)^100
(63)^7 : 63 = 3²*7 : (63)^7 = 3^14 *7
(49)^4 = (7²)^4 = 7^8
on obtient b= 2^300*3^14*5^100*7^8*11
je bloque sur
b)Factoriser A-B
un peu d'aide SVP merciiii
Avec la decomposition en produit de nombres premiers
11 messages
- Page 1 sur 1
m pokora a écrit:Bonjour je bloque sur cette exercice et je vous demande un peu d'aide s'il vous plait sur ça :
On se propose de comparer les entiers naturels:
A=13x8^100x(25)^50x(21)^15
B=11x4^100x10^100x(63)^7x(49)^4
1.Avec le signe de la différence
a)Décomposer A et B en produit de nombres premiers
b)Factoriser A-B
c)En déduire le signe de A-B
d)Comparer alors A et B
2.Avec un quotient
a)En utilisant la question 1.a), donner la fraction irréductible égale à A/B
b)Comparer alors A et B.
j'ai fait : A)
8 = 2^3 donc 8^100 = (23)^100 = 2^300
( 25 )^50= 5²= (25)^50 = 5^100
(21)^15 : 21 = 3 x 7 = (21)15 = 3^15 x 7^15
on obtient : A = 2^300 x 3^15 x 5^100 x 7^15 x 13
B) 4= 2² = 2^200
10^100 : 10 = (2*5)^100
(63)^7 : 63 = 3²*7 : (63)^7 = 3^14 *7
(49)^4 = (7²)^4 = 7^8
on obtient b= 2^300*3^14*5^100*7^8*11
je bloque sur
b)Factoriser A-B
un peu d'aide SVP merciiii
Est-ce que tu pourrais mettre des parenthèses sur les exposants, s'il te plait ? Ou tout simplement écrire avec les balises TeX. C'est trop illisible pour moi :triste:
On se propose de comparer les entiers naturels:
A=13x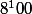 x(25)^50x
x(25)^50x^15)
B=11x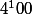 x
x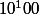 x
x^7) x
x^4)
1.Avec le signe de la différence
a)Décomposer A et B en produit de nombres premiers
b)Factoriser A-B
c)En déduire le signe de A-B
d)Comparer alors A et B
2.Avec un quotient
a)En utilisant la question 1.a), donner la fraction irréductible égale à A/B
b)Comparer alors A et B.
j'ai fait : A)
8 =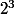 donc
donc 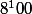 =
= ^100 = 2^300)
^50= 5^2= (25)^50 = 5^100)
^15 : 21 = 3* 7 = (21)15 = 3^15 * 7^15)
on obtient : A =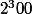 x
x  *
* 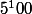 x
x x 13
x 13
B) 4= 2² =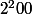
10^100 : 10 = (2*5)^100
^7) : 63 = 3²*7 :
: 63 = 3²*7 : ^7 = 3^14) *7
*7
^4) =
= ^4 = 7^8)
on obtient b=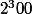 *
*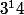 *
*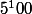 *
*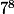 *11
*11
je bloque sur
b)Factoriser A-B
j'espere que c'est bon je suis nul en
A=13x
B=11x
1.Avec le signe de la différence
a)Décomposer A et B en produit de nombres premiers
b)Factoriser A-B
c)En déduire le signe de A-B
d)Comparer alors A et B
2.Avec un quotient
a)En utilisant la question 1.a), donner la fraction irréductible égale à A/B
b)Comparer alors A et B.
j'ai fait : A)
8 =
on obtient : A =
B) 4= 2² =
10^100 : 10 = (2*5)^100
on obtient b=
je bloque sur
b)Factoriser A-B
j'espere que c'est bon je suis nul en
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


 : 63 = 3²*7 :
: 63 = 3²*7 :  *7
*7
