Un autre corps est ce possible ?

par **J-R** » 18 Aoû 2007, 15:57

bonjour,

j'ai été pris de curiosité :id: en lisant cette phrase:

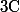
, ensemble des nombres a+ib avec correspond à l'ensemble des points d'un plan.

par consséquent, selon moi il devrait exister un autre corps dans lequel les nombres correspondraient à l'espace ?
Si il y a existence de ce corps, j'aimerais en toucher 2 mots (ca se voit quand, quel type de nombres ou une page internet qui détaille bien ....)

merci

par **Nightmare** » 18 Aoû 2007, 15:59

Bonjour, très bonne intuition.

Ce corps dont tu parles est le corps des quaternions noté

. On ne le voit pas au lycée et très peu en prépa car les quaterions sont assez dûrs à manier, ne serait-ce que parce que ce corps n'est pas commutatif

par **J-R** » 18 Aoû 2007, 16:01

bonjour nightmare et merci,

les quaternions je regarde sur wiki et si j'ai des questions...

a+

par **J-R** » 18 Aoû 2007, 16:06

Cette découverte entraîna l'abandon de l'utilisation exclusive des lois commutatives

lois commutative, as tu une définition simple, concrete de la commutativité ? Faut il l'entendre comme la multiplication ou l'addition : a+b=b+a ou a*b=b*a ?

par **Nightmare** » 18 Aoû 2007, 16:12

oui c'est ça. Une loi * est dite commutative si pour tout éléments a et b, a*b=b*a.

La multiplication et l'addition usuelles sont commutatives.
La composition de fonction n'est pas commutative.

par **J-R** » 18 Aoû 2007, 16:23

ok

sinon c'est vrai que c'est assez marrant à manipuler notamment pour le produit....

c'est bon j'ai lu ccce que je voulais savoir

merci Nightmare

pour ceux que ca intéresse:

par **quinto** » 18 Aoû 2007, 16:34

Oui,
en fait ce n'est pas vraiment une représentation de l'espace, mais une représentation d'un espace à 4 "dimensions".

par **kazeriahm** » 18 Aoû 2007, 16:56

il y avait pas d'ailleurs un théorème établissant qu'on ne peut trouver de corps de dimension 3 (en tant qu'ev sur R, à isomorphisme près), ou quelque chose dans ce gout la ?

par **J-R** » 18 Aoû 2007, 17:04

quinto a écrit:Oui,
en fait ce n'est pas vraiment une représentation de l'espace, mais une représentation d'un espace à 4 "dimensions".

4 dimensions ?

(je connais le temps mais là pour moi je ne vois pas le rapport....)

par **Nightmare** » 18 Aoû 2007, 17:06

Tu as des notions d'espace vectoriel J-R ?

par **anima** » 18 Aoû 2007, 17:09

Nightmare a écrit:Tu as des notions d'espace vectoriel J-R ?

J'en ai. Donc rien n'est perdu coté explications, surtout que je viens aussi de découvrir l'ensemble des quaternions... Et ca me branche pas mal :we:

par **Nightmare** » 18 Aoû 2007, 17:14

Ben c'est juste que H est un R-ev de dimension 4 et non 3 comme on pourrait le penser.

par **anima** » 18 Aoû 2007, 17:20

Nightmare a écrit:Ben c'est juste que H est un R-ev de dimension 4 et non 3 comme on pourrait le penser.

Ca j'avais compris avec l'article de wikipedia, mais bon... C'est la base. Apres, il doit y avoir des applications bien spécifiques, et c'est ca qui m'intrigue. Enfin remarque, j'avais déja croisé le terme d'"hypercomplexe" dans un bouquin. J'essayerai de retrouver lequel.

par **J-R** » 18 Aoû 2007, 17:30

je sais juste que c'est théorique, et que c'est un espace régit par des lois (comme on a dit commutativité, associativité...) je sais que ca...

merci :)

par **kazeriahm** » 18 Aoû 2007, 17:54

pas si théorique que ca puisqu'il parait que ca sert beaucoup en quantique :help:

par **quinto** » 18 Aoû 2007, 18:12

kazeriahm a écrit:pas si théorique que ca puisqu'il parait que ca sert beaucoup en quantique :help:

En quantique et en ballistique.
Il faut se dire que malgré ce que l'on pense, les maths servent à peu près partout et que presque tout sujet mathématique s'applique ou s'appliquera un jour ...

par **J-R** » 18 Aoû 2007, 18:19

alors un ev c'est quoi concrètment ?

par **kazeriahm** » 18 Aoû 2007, 18:22

il y a pas de "concrètement" qui tienne :we:

un ev c'est un groupe muni d'une multiplication externe vérifiant ......

il faut considèrer ces objets mathématiques comme tels, c'est d'ailleurs ca qu'on apelle l'abstraction, le fait qu'on ne puisse pas rapprocher les maths avec le sensible (enfin... je me comprend)

par **J-R** » 18 Aoû 2007, 18:40

n ev c'est un groupe muni d'une multiplication externe vérifiant ......

intuitivement (ca va mieu ?

)

là je ne comprend pas .... :doh:

par **Nightmare** » 18 Aoû 2007, 18:41

Ben pour bien comprendre ce que sont les ev il faut avoir aussi des notions de structures sur les ensembles (Groupes, anneaux, corps etc...). Ne pas aller plus vite que la musique :lol3:

Un autre corps est ce possible ?

un autre corps est ce possible ?

Qui est en ligne