Asymptote oblique

[barbara34]

Bonjour, y aurait-il une personne pouvant m'expliquer comment trouver a et b dans le cas d'une asymptote oblique ?

Je connais mon cours mais je n'arrives pas à l'appliquer ...

Un grand merci d'avance !! :we:

[nodjim]

le "a" de asymptote, c'est la 1ère lettre, et le "b" de oblique, c'est la seconde.
Plus sérieusement, qu'est ce donc que ces a et b ?

[biss]

Une des methode parois d'autre eedt de mettre sous la forme
Une autre consiste a faire en l'infini puis de faire en l'infini aussi

[barbara34]

le "a" de asymptote, c'est la 1ère lettre, et le "b" de oblique, c'est la seconde.
Plus sérieusement, qu'est ce donc que ces a et b ?

a est le coefficient de la droite et b une constante. mais comment trouver leurs valeurs ?

[barbara34]

Une des methode parois d'autre eedt de mettre sous la forme
Une autre consiste a faire en l'infini puis de faire en l'infini aussi

je ne connaissais pas la première méthode c'est la deuxième que j'ai du mal

[nodjim]

Des exemples ?

[biss]

Tu as une fonction ? Tu divise par x et tu fais la limite en l'infini c'est tout

[barbara34]

Des exemples ?

comme exemple: f(x)= x (au carré) - 9 / 2x + 5

trouver l'asymptote oblique ...

[Robot]

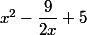
(c'est ce que tu as écrit) n'a pas d'asymptote oblique, juste une asymptote verticale.
Utilise les parenthèses pour écrire ce que tu voudrais écrire !

[barbara34]

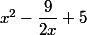
(c'est ce que tu as écrit) n'a pas d'asymptote oblique, juste une asymptote verticale.
Utilise les parenthèses pour écrire ce que tu voudrais écrire !

oui pardon,
(x^2-9) / (2x-5)

[Robot]

Fais la division euclidienne du numérateur par le dénominateur.

[barbara34]

Fais la division euclidienne du numérateur par le dénominateur.

je ne sais plus la faire ....

[Black Jack]

f(x) = (x^2-9) / (2x-5)

Méthode 1)

Division euclidienne ...

f(x) = x/2 + 5/4 - (11/4)/(2x-5)

asymptote oblique en -oo et en +oo : y = x/2 + 5/4

-----
Méthode 2:

a = lim(x--> +/- oo) (f(x)/x) = lim(x--> +/-oo) (x^2-9) / (2x²-5x) = 1/2

b = lim(x--> +/- oo) (f(x) - a.x) = lim(x--> +/- oo) [(x^2-9) / (2x-5) - x/2] = lim(x--> +/- oo) [(2x²-18 - 2x²+5x)/(2(2x-5))] = lim(x--> +/- oo) [(5x -18)/(4x-10)] = 5/4

asymptote oblique en -oo et en +oo : y = ax + b soit y = x/2 + 5/4
-----
:zen:

[fibonacci]

Bonjour;



il n'y a pas de facteur en x d'où:





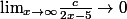
d'où la droite asymptotique:



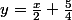
"on pourrait dire que c'est la droite tangente à l'infini de f(x)"

les deux méthodes précédentes sont plus "naturelles"

[Robot]

je ne sais plus la faire ....

Alors tu as intérêt à réviser !

[barbara34]

Bonjour;



il n'y a pas de facteur en x d'où:





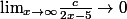
d'où la droite asymptotique:



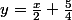
"on pourrait dire que c'est la droite tangente à l'infini de f(x)"

les deux méthodes précédentes sont plus "naturelles"

Merci pour ton aide vraiment

[barbara34]

Bonjour;



il n'y a pas de facteur en x d'où:





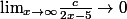
d'où la droite asymptotique:



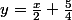
"on pourrait dire que c'est la droite tangente à l'infini de f(x)"

les deux méthodes précédentes sont plus "naturelles"

Au top merci !!!

[barbara34]

f(x) = (x^2-9) / (2x-5)

Méthode 1)

Division euclidienne ...

f(x) = x/2 + 5/4 - (11/4)/(2x-5)

asymptote oblique en -oo et en +oo : y = x/2 + 5/4

-----
Méthode 2:

a = lim(x--> +/- oo) (f(x)/x) = lim(x--> +/-oo) (x^2-9) / (2x²-5x) = 1/2

b = lim(x--> +/- oo) (f(x) - a.x) = lim(x--> +/- oo) [(x^2-9) / (2x-5) - x/2] = lim(x--> +/- oo) [(2x²-18 - 2x²+5x)/(2(2x-5))] = lim(x--> +/- oo) [(5x -18)/(4x-10)] = 5/4

asymptote oblique en -oo et en +oo : y = ax + b soit y = x/2 + 5/4
-----
:zen:

Genial merci beaucoup

[Sylviel]

Fais la division euclidienne du numérateur par le dénominateur.

Divisio euclidienne de polynomes au lycée :doh: :doh: