Asymptote oblique/postion

[Anonyme]

Bonsoir,

je dois montrer que la droite déquation y=2x est asymptote a fetc.... ok ca c'est fais.
après on me demande d'étudier la position de (C) par rapport a cette asymptote oblique, donc voila les renseignements:
f(x)=
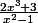
donc pour savoir leurs positions, j'ai fais f(x)-2x et je trouve

et je ne sais pas quoi faire avec ca

Merci de me donner un coup de pattes et de m'éclaircir

[LN1]

Bonsoir,

tu construis tout simplement un tableau de signe (signe de 2x + 3, signe de x² - 1)

si f(x) - 2x > 0 alors Cf est au dessus de (D)
si ...

Bon courage

[Chimerade]

Bonsoir,

je dois montrer que la droite déquation y=2x est asymptote a fetc.... ok ca c'est fais.
après on me demande d'étudier la position de (C) par rapport a cette asymptote oblique, donc voila les renseignements:
f(x)=
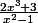
donc pour savoir leurs positions, j'ai fais f(x)-2x et je trouve

et je ne sais pas quoi faire avec ca

Merci de me donner un coup de pattes et de m'éclaircir

Et si tu mettais x en facteur au numérateur et x² en facteur au dénominateur !

[allomomo]

Salut,






Donc f admet une asymptote à C d'équation

Pour étudier la position relative de C/ Asy, il faut étudier le signe de x=(-3/2)

sur ]-oo ; -3/2[, f(x) > 2x ::: donc la courbe C est au-dessus de l'Asy
sur ]-3/2 ; +oo[, f(x) < 2x ::: donc la courbe C est au-dessous de l'Asy

[LN1]

attention,

le signe dyu dénominateur importe aussi (x² - 1) donc ... tableau de signe