Bonjour à tous et à toutes.
Puisque je dois vendre mon livre de terminale, je voudrais bien finir tous les défis qu'il y a dedans. Pour le moment, je remercie raito et gaara d'essayer d'en avoir fait avec moi quelques uns.
Mais là on bloque gaara et moi sur un défi pourri calculatoire:
Déterminer la dérivée n-ième de la fonction f:x-->[sinx]^3 + [cosx]^3 définie sur R.
Pour le moment, j'ai trouvé pour n=2k:
f'(2k)(x) = (-1)^k * 3^2k [(cosx)^3 + (sinx)^3^] + (expression à trouver)(cosx-sinx).
f'('2k+1)(x)= (-1)^k * 3^(2k+1) [(sinx)^3 - (cosx)^3^] + (expression à trouver) (cos x - sinx).
Merci pour votre aide :marteau:
A l'assaut des problèmes ouverts ^^
32 messages
- Page 1 sur 2 - 1, 2
par Clembou » 30 Juil 2008, 21:18
Ruch a écrit:Bonjour à tous et à toutes.
Puisque je dois vendre mon livre de terminale, je voudrais bien finir tous les défis qu'il y a dedans. Pour le moment, je remercie raito et gaara d'essayer d'en avoir fait avec moi quelques uns.
Mais là on bloque gaara et moi sur un défi pourri calculatoire:
Déterminer la dérivée n-ième de la fonction f:x-->[sinx]^3 + [cosx]^3 définie sur R.
Pour le moment, j'ai trouvé pour n=2k:
f'(2k)(x) = (-1)^k * 3^2k [(cosx)^3 + (sinx)^3^] + (expression à trouver)(cosx-sinx).
f'('2k+1)(x)= (-1)^k * 3^(2k+1) [(sinx)^3 - (cosx)^3^] + (expression à trouver) (cos x - sinx).
Merci pour votre aide :marteau:
Il faut poser le problème :
Tu as déjà calculer
par Flodelarab » 30 Juil 2008, 21:51
D'abord, je déteste faire la dérivée d'un produit quand je n'en étudie pas le signe après.
Première étape: linéariser.
Première étape: linéariser.
par Ruch » 30 Juil 2008, 21:53
Ben oui sinon je n'aurais pas trouvé les solutions. Elles peuvent pas tomber du ciel ^^
Sinon, je rappelle que la dérivé nième ne doit pas s'exprimer en fonction de f (c'est un peu le principe de ces types d'exercices).
Donc ça ne sert à rien de remarque que f''(x) = -3f(x) + 2f'(x)...
Merci.
Sinon, je rappelle que la dérivé nième ne doit pas s'exprimer en fonction de f (c'est un peu le principe de ces types d'exercices).
Donc ça ne sert à rien de remarque que f''(x) = -3f(x) + 2f'(x)...
Merci.
par Ruch » 30 Juil 2008, 21:56
En réponse à Flo, j'ai utilisé la formule cos²x + sin²x = 1.
Mais tu as trouvé quelque chose en linéarisant (parce que c'est un peu chiant de se taper des calculs un peu longs...)?
Enfin, je vais essayer de linéariser et je tiens au courant. Sinon, il n'est pas interdit de suivre notre piste :++:
Mais tu as trouvé quelque chose en linéarisant (parce que c'est un peu chiant de se taper des calculs un peu longs...)?
Enfin, je vais essayer de linéariser et je tiens au courant. Sinon, il n'est pas interdit de suivre notre piste :++:
par Clembou » 30 Juil 2008, 22:04
miikou a écrit:Le titre avait l'air prometteur pourtant, dommage :--:
Tu croyais qu'on allait démontrer la conjecture de Syracuse ?? :doh: :triste: Faut pas rêver ! :ptdr:
par _-Gaara-_ » 30 Juil 2008, 22:13
Clembou a écrit:Tu croyais qu'on allait démontrer la conjecture de Syracuse ?? :doh: :triste: Faut pas rêver ! :ptdr:
arf.. je l'ai démontrée de tête en me rasant la barbe ! :ptdr:
par _-Gaara-_ » 30 Juil 2008, 22:13
miikou a écrit:Le titre avait l'air prometteur pourtant, dommage :--:
lol aurais tu un conseil à donner ou ??
par Flodelarab » 30 Juil 2008, 22:48
C'est vrai que linéariser par les formules trigonométriques classiques est fastidieux.
Si tu connais les complexes, je te conseille tout particulièrement les formules d'Euler.
=cos^3(x) + sin^3(x))
=(\frac{e^{ix}+e^{-ix}}{2})^3 + (\frac{e^{ix}-e^{-ix}}{2i})^3)
=\frac{1}{8}[(e^{ix}+e^{-ix})^3 + (-ie^{ix}+ie^{-ix})^3])
=\frac{1}{8}[e^{3ix}+3e^{ix}+3e^{-ix}+e^{-3ix}+ie^{3ix}-3ie^{ix}+3ie^{-ix}-ie^{-3ix}])
=\frac{1}{8}[2cos(3x)+6cos(x)-2sin(3x)+6sin(x)])
=\frac{1}{4}[cos(3x)+3cos(x)-sin(3x)+3sin(x)])
=\frac{1}{4}[cos(3x)-sin(3x)+3cos(x)+3sin(x)])
Plus facile à dériver.
Si tu connais les complexes, je te conseille tout particulièrement les formules d'Euler.
Plus facile à dériver.
par Ruch » 30 Juil 2008, 23:06
Euh oui je connais les formules d'Euleur (on en fait quand même en terminale ^^) :++:
Alors en linéarisant, j'ai l'impression qu'il va y avoir une discjonction de cas jusqu'à 4k (genre 4k+1, 4k+2 et 4k+3).
En fait je trouve ça :
f'(x) = 3/4 (cosx - cos3x - sin3x -sinx)
f''(x) = 3/4 (-sinx + 3sin3x - 3cos3x - cosx)
f'''(x)= 3/4 (-cosx + 9cos3x + 9 sin3x + sinx)
f(4)x= 3/4 (sinx - 27sin3x + 27cos3x + cosx)
f(5)x= 3/4 (cos x - 81cos3x - 81sin3x - sinx)
Si n=4k
f(n)(x) = 3/4 (cosx - 3^(n-1)cos3x - 3^(n-1)sin3x - sinx)
De même pour n=4k+1, 4k+2 et 4k+3, on replace à chaque foit par 3^(n-1).
Reste à démontrer tout ça par récurence, ce qui va être très fastidieux. A mon avis, on peut diviser ça en 2 cas comme je l'ai fait en haut. J'arrive pas à trouver l'expression manquante....
Alors en linéarisant, j'ai l'impression qu'il va y avoir une discjonction de cas jusqu'à 4k (genre 4k+1, 4k+2 et 4k+3).
En fait je trouve ça :
f'(x) = 3/4 (cosx - cos3x - sin3x -sinx)
f''(x) = 3/4 (-sinx + 3sin3x - 3cos3x - cosx)
f'''(x)= 3/4 (-cosx + 9cos3x + 9 sin3x + sinx)
f(4)x= 3/4 (sinx - 27sin3x + 27cos3x + cosx)
f(5)x= 3/4 (cos x - 81cos3x - 81sin3x - sinx)
Si n=4k
f(n)(x) = 3/4 (cosx - 3^(n-1)cos3x - 3^(n-1)sin3x - sinx)
De même pour n=4k+1, 4k+2 et 4k+3, on replace à chaque foit par 3^(n-1).
Reste à démontrer tout ça par récurence, ce qui va être très fastidieux. A mon avis, on peut diviser ça en 2 cas comme je l'ai fait en haut. J'arrive pas à trouver l'expression manquante....
par Skullkid » 30 Juil 2008, 23:31
La démonstration par récurrence est-elle absolument nécessaire ? On peut admettre (ou même le démontrer, et là ça reste très court) qu'on connaît la dérivée n-ième de cos (donc de sin) selon la valeur de n modulo 4. A partir de là et de la formule linéarisée qu'a donnée Flodelarab, le résultat est immédiat (la dérivée n-ième d'une somme est la somme des dérivées n-ièmes...).
par jomanaomar » 30 Juil 2008, 23:39
bonjour tout le monde
Y = (sin x + cos x) (sin^2 x + cos^2 x sin x cos x)
Y = (sin x + cos x) (1 sin x cos x)
Y = (sin x + sin (pi/2 -x) )(1 1/2 sin 2x)
Y = (2sin pi/4 cos (x-pi/4) )(1 1/2 sin 2x)
Y = ;)2 cos (x-pi/4)(1 1/2 sin 2x)
Y = ;)2 cos (x-pi/4) - ;)2/2 sin 2x cos (x-pi/4)
Y = ;)2 cos (x-pi/4) - ;)2/4 sin (3x-pi/4) - ;)2/4 cos (x+pi/4)
Puis complète
Y = (sin x + cos x) (sin^2 x + cos^2 x sin x cos x)
Y = (sin x + cos x) (1 sin x cos x)
Y = (sin x + sin (pi/2 -x) )(1 1/2 sin 2x)
Y = (2sin pi/4 cos (x-pi/4) )(1 1/2 sin 2x)
Y = ;)2 cos (x-pi/4)(1 1/2 sin 2x)
Y = ;)2 cos (x-pi/4) - ;)2/2 sin 2x cos (x-pi/4)
Y = ;)2 cos (x-pi/4) - ;)2/4 sin (3x-pi/4) - ;)2/4 cos (x+pi/4)
Puis complète
par Ruch » 30 Juil 2008, 23:48
Ah non c'est bon j'ai enfin trouvé ! Pas la peine d'une disjonction en 4 cas, en 2 cas ça suffit. En fait, j'ai trouvé la formule manquante dans mon expression.
J'explique:
En utilisant la formule cos²x + sin²x = 1 et en calculant les 4 dérivées premières:
f(1)(x) = 3[(sinx)^3 - (cosx)^3^] + 3(cosx - sinx)
f(2)(x) = -9[(cosx)^3 + (sinx)^3^] + 6 (cosx + sinx)
f(3)(x) = -27[(sinx)^3 - (cosx)^3^] - 21(cosx - sinx)
f(4)(x) = 81[(cosx)^3 + (sinx)^3^] - 60(cosx + sinx)
Pour le coeff1, pas de problème, on a fixé l'expression en fonction de n.
Pour le coeff2, on remarque : 3 // 3²-3=6 // 3^3-3²+3=-21 // 3^4-3^3+3²-3=-60.
Donc si n= 2k ,coeff2= (-1)^k 3/4 (1-2^k) .
si n=2k+1, coeff2 = (-1)^k 3/4 [1+3^(2k+1)]
(On trouve ces expression par somme de suites géométriques).
Donc:
Si n = 2k,
f'(2k)(x) = (-1)^k * 3^2k [(cosx)^3 + (sinx)^3^] + (-1)^k 3/4 (1-2^k) (cosx-sinx).
Si n=2k+1
f'('2k+1)(x)= (-1)^k * 3^(2k+1) [(sinx)^3 - (cosx)^3^] + (-1)^k 3/4 [1+3^(2k+1)] (cos x - sinx).
Et c'est aisément démontrable par récurrence :++:
J'explique:
En utilisant la formule cos²x + sin²x = 1 et en calculant les 4 dérivées premières:
f(1)(x) = 3[(sinx)^3 - (cosx)^3^] + 3(cosx - sinx)
f(2)(x) = -9[(cosx)^3 + (sinx)^3^] + 6 (cosx + sinx)
f(3)(x) = -27[(sinx)^3 - (cosx)^3^] - 21(cosx - sinx)
f(4)(x) = 81[(cosx)^3 + (sinx)^3^] - 60(cosx + sinx)
Pour le coeff1, pas de problème, on a fixé l'expression en fonction de n.
Pour le coeff2, on remarque : 3 // 3²-3=6 // 3^3-3²+3=-21 // 3^4-3^3+3²-3=-60.
Donc si n= 2k ,coeff2= (-1)^k 3/4 (1-2^k) .
si n=2k+1, coeff2 = (-1)^k 3/4 [1+3^(2k+1)]
(On trouve ces expression par somme de suites géométriques).
Donc:
Si n = 2k,
f'(2k)(x) = (-1)^k * 3^2k [(cosx)^3 + (sinx)^3^] + (-1)^k 3/4 (1-2^k) (cosx-sinx).
Si n=2k+1
f'('2k+1)(x)= (-1)^k * 3^(2k+1) [(sinx)^3 - (cosx)^3^] + (-1)^k 3/4 [1+3^(2k+1)] (cos x - sinx).
Et c'est aisément démontrable par récurrence :++:
par Ruch » 30 Juil 2008, 23:53
La démonstration par récurrence est-elle absolument nécessaire ? On peut admettre (ou même le démontrer, et là ça reste très court) qu'on connaît la dérivée n-ième de cos (donc de sin) selon la valeur de n modulo 4. A partir de là et de la formule linéarisée qu'a donnée Flodelarab, le résultat est immédiat (la dérivée n-ième d'une somme est la somme des dérivées n-ièmes...).
Oui tu as raison, je suis d'accord.
Mais bon, nous voilà avec 2 solutions possibles du problèmes :we:
PS: jomanaomar, je verrais ça, pour le moment, ma tête va exploser de calculs^^
par Flodelarab » 31 Juil 2008, 10:00
Mouai. Sinon, on cherche une suite de période 4 qui fasse 1 1 -1 -1
Il y en a une toute trouvée:
))
}(x)= \frac{\sqrt{2}}{4}(3^n( sin(\frac{\pi}{4}(5+2n))sin(3x)+ sin(\frac{\pi}{4}(3+2n))cos(3x))+3( sin(\frac{\pi}{4}(5+2n))sin(x)+ sin(\frac{\pi}{4}(1+2n))cos(x))))
Ça doit se simplifier ... si le cur vous en dit.
Il y en a une toute trouvée:
Ça doit se simplifier ... si le cur vous en dit.
par _-Gaara-_ » 31 Juil 2008, 10:06
Flodelarab a écrit:Mouai. Sinon, on cherche une suite de période 4 qui fasse 1 1 -1 -1
Il y en a une toute trouvée: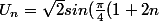
Wahhou !! ne me dis pas que c'est la première suite à laquelle tu as pensé :doh:
pour ma part j'essayais de faire +1 , -1 pour trouver et il s'avère qu'il y a ça
non mais c'est fou, il n'y a pas une réponse qu'un gars normal en maths puisse comprendre ? (genre moi ?)
par Flodelarab » 31 Juil 2008, 11:39
_-Gaara-_ a écrit:Wahhou !! ne me dis pas que c'est la première suite à laquelle tu as pensé :doh:
Ben bien sûr que si !
Tu cherches une fonction périodique, donc tu penses aux fonctions trigo. Sinus par exemple.
Tu cherches une fonction de période 4. Or les fonctions trigo sont de période 2Pi donc tu divises en 4 et tu trouves un pas de Pi/2.
Tu cherches sin(x)=sin(x+Pi/2). Donc x=Pi/4
Reste plus qu'à normaliser. Donc on divise par sin(Pi/4)
Facile, non ?
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :