Bonjour,
J'ai actuellement un exercice sur les suites à résoudre mais je pose plutôt une question générale.
Dnas certains exercices traitant des suites numériques, il faut parfois être amené à trouver l'entier naturel n pour lequel une relation est vérifiée.
Un exemple : soit
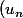 : u_{n} = 16n^{2} + 12n - 2)
. Trouver la plus petite valeur de n pour laquelle

. J'ai bien conscience qu'il faut ramener ça à un polynôme, de résoudre en fait 16x² + 12x - 102 = 0, d'utiliser le discriminant, cependant les racines que je trouve sont bien entendu réelles et ce ne sont pas des entiers naturel.
EDIT : (Après réflexion, je viens de m'apercevoir que ça à a voir avec le signe du polynôme dans cet exemple et par la même occasion que cet exemple était pas terrible, mais c'est pour le principe).Comment rédiger proprement le fait qu'il faut prendre obligatoirement un entier supérieur ? Je ne veux absolument pas calculer par exemple (si ma racine vaut 10,48)
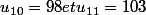
et conclure en disant qu'il faut prendre n = 11. Cela me rapelle le tatonnement pour trouver les solutions de

par exemple, ce dont j'ai horreur. Pour ce dernier exemple, j'ai découvert qu'on pouvait faire descendre la puissance avec ln et donc résoudre l'inéquation normalement. Existe-t-il une méthode similaire pour répondre correctement à mon problème ?
Merci.
