Arithmétique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
fetdak
- Messages: 5
- Enregistré le: 02 Sep 2007, 18:50
-
 par fetdak » 02 Sep 2007, 19:38
par fetdak » 02 Sep 2007, 19:38
Bonjour
j'ai un probleme dans la question 3-c de l'exercice suivant
Soit n un entier naturel
1- Déterminer pour tout entier n de {0,1,...,6} le reste modulo 7 de

2- Montrer que
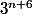
-

est divisible par 7
3-a- Calculer le reste modulo 7 de
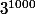
b- Quel est le chiffre des unités de
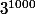
?
c- Soit s la somme des chiffres du nombre
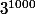
.
Quel est le reste modulo 7 de s ?
Pouvez vous m'aider S.V.P
Merci
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 02 Sep 2007, 19:44
par Flodelarab » 02 Sep 2007, 19:44
Bien vu d'utiliser Latex. Juste un conseil, pour qu'une expression soit pris en entier, mets la entre accolades. Sinon, il ne prend que le premier chiffre
ex: {1000}
Sinon, peux tu nous donner tes réponses précédentes pour qu'on puisse traiter directement la 3-c ? merci
-
fetdak
- Messages: 5
- Enregistré le: 02 Sep 2007, 18:50
-
 par fetdak » 02 Sep 2007, 20:30
par fetdak » 02 Sep 2007, 20:30
Voici les reponses :
1- si n=6k

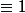
(7)
si n=6k+1


(7)
si n=6k+2


(7)
si n=6k+3


(7)
si n=6k+4


(7)
si n=6k+5


(7)
2- Puisque 7 est un nombre premier et 3 n'est pas divisible par 7 donc d'apres
le Petit Théorème de Fermat on a:
)
donc
)
donc
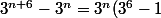 \equiv 0 (7))
3-a-

on a
)
et
)
donc
)
b- On a:
)
)
)
)
avec
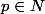
Puisque
)
d'où le chiffre des unités est 1
Voila! j'espere que j'ai bien ecris en Latex
Merci d'avance
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 03 Sep 2007, 13:53
par Flodelarab » 03 Sep 2007, 13:53
J'ai exploré 2-3 idées comme 3=10-7 ou 3*3+1=10 mais je n'ai pas abouti.
Je ne sais pas.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 03 Sep 2007, 17:02
par Flodelarab » 03 Sep 2007, 17:02
La réponse est 2142 puisque 3^1000=1322070819480806636890455259752144365965422032752148167664920368226828597346704899540778313850608061963909777696872582355950954582100618911865342725257953674027620225198320803878014774228964841274390400117588618041128947815623094438061566173054086674490506178125480344405547054397038895817465368254916136220830268563778582290228416398307887896918556404084898937609373242171846359938695516765018940588109060426089671438864102814350385648747165832010614366132173102768902855220001
Mais c pas trop ce qu'on demande
-
fetdak
- Messages: 5
- Enregistré le: 02 Sep 2007, 18:50
-
 par fetdak » 03 Sep 2007, 17:17
par fetdak » 03 Sep 2007, 17:17
comment vous avez fait pour calculer
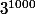
?
non je blague bien sur!
je suis en train de chercher sur le net s'il y a des exercices qui ressemblent à celui ci ... c'est à dire où on trouve
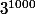
et le modulo 7
connaissez vous des adresses que je peux visiter ?
Merci d'etre interessé par mon exercice
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 03 Sep 2007, 17:19
par rene38 » 03 Sep 2007, 17:19
Salut
Quel est le reste modulo 7 de s ?
Flodelarab a écrit:La réponse est 2142
Je ne crois pas (
mais je n'ai pas la réponse ...)
-
fetdak
- Messages: 5
- Enregistré le: 02 Sep 2007, 18:50
-
 par fetdak » 03 Sep 2007, 17:27
par fetdak » 03 Sep 2007, 17:27
c'est peut etre la bonne reponse ! je ne sais pas
mais j'ai besoin d'une demonstration
merci
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 03 Sep 2007, 17:32
par Flodelarab » 03 Sep 2007, 17:32
rene38 a écrit:Salut Je ne crois pas (mais je n'ai pas la réponse ...)
Tu ne peux pas me contredire alors que je te donnes in extenso l'écriture du nombre en base 10 ....
C'est juste, c sur.
Mais le but de l'arithmétique est de trouver sans faire le calcul... sinon ça n'a pas d'interet
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 03 Sep 2007, 17:38
par Flodelarab » 03 Sep 2007, 17:38
Ah oui pardon. J'ai oublié le modulo :lol:
Ben c'est 0 alors
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 03 Sep 2007, 17:38
par Joker62 » 03 Sep 2007, 17:38
Je pense juste qu'il voulait dire que tu réponds pas à la question en sachant qu'on demande le reste modulo 7 qui est donc 0
Vu que 2142 est multiple de 7
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Sep 2007, 14:01
par Clembou » 04 Sep 2007, 14:01
fetdak a écrit:Bonjour
j'ai un probleme dans la question 3-c de l'exercice suivant
Soit n un entier naturel
1- Déterminer pour tout entier n de {0,1,...,6} le reste modulo 7 de

2- Montrer que
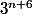
-

est divisible par 7
3-a- Calculer le reste modulo 7 de
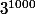
b- Quel est le chiffre des unités de
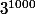
?
c- Soit s la somme des chiffres du nombre
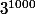
.
Quel est le reste modulo 7 de s ?
Pouvez vous m'aider S.V.P
Merci
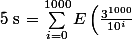)
Après, on peut peut-être utiliser la propriété qui dit :
Si
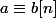
et

alors :

-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 04 Sep 2007, 14:04
par Flodelarab » 04 Sep 2007, 14:04
Clembou a écrit: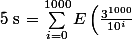)
Après, on peut peut-être utiliser la propriété qui dit :
Si
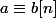
et

alors :

Utilises aussi la réponse à la question 3b...
Pourquoi penses tu que s a 1000 chiffres ?
Peux tu détailler ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Sep 2007, 14:09
par Clembou » 04 Sep 2007, 14:09
Flodelarab a écrit:Pourquoi penses tu que s a 1000 chiffres ?
Peux tu détailler ?
Ah non ! Erreur de ma part ! Excusez-moi ! Je réflechis encore, je vous tiens au courant de mes avancées...
Après moultes recherches, j'arrive à la conclusion que la somme des chiffres de
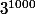
est congru à 0 modulo 3.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Sep 2007, 15:09
par Clembou » 04 Sep 2007, 15:09
Début de réflexion (vous me corrigez si j'ai faux) :
Soit :

Donc :
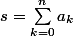
Or calculons les restes de
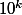
modulo 7 :






...
On sait aussi que :

Donc :

Or : le chiffres des unités de
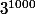
est 1 donc
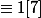

Le tout est de calculer

et on peut arriver au résultat que propose Flodelarab...
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 06 Sep 2007, 18:02
par lapras » 06 Sep 2007, 18:02
Oui mais comment calculer ce n ? Je trouve que cet exo est corcé vers la fin !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
