Bonjour ,
on me demande quels sont le quotient et le reste dans la division par 2^23 + 2 + 1 de 2^40 + 2^28 + 2^23 + 2^20 + 2^18 + 2^17 + 2^6 + 2^5 + 2 + 1
Merci pour votre aide
Cordialement
Arithmétique division
3 messages
- Page 1 sur 1
Re: arithmétique division
Comme tu as affaire à des puissances de 2, c'est comme ci tu ôtais plusieurs fois (23,1,0) à (40,28,23,20,18,17,6,5,1,0)
(40,28,23,20,18,17,6,5,1,0)- (23,1,0) = (40,28,20,18,17,6,5)
(40,28,20,18,17,6,5) - (5)(23,1,0)=(40,28,20,18,17,6,5)-(28,6,5)=(40,20,18,17)
(40,20,18,17)-(17)(23,1,0)=(40,20,18,17)-(40,18,17)=(20)
(40,28,23,20,18,17,6,5,1,0)- (23,1,0) = (40,28,20,18,17,6,5)
(40,28,20,18,17,6,5) - (5)(23,1,0)=(40,28,20,18,17,6,5)-(28,6,5)=(40,20,18,17)
(40,20,18,17)-(17)(23,1,0)=(40,20,18,17)-(40,18,17)=(20)
Re: arithmétique division
Salut,
Faire la "division Euclidienne" de (entier relatif) par
(entier relatif) par  (entier naturel non nul), ça veut dire arriver à écrire
(entier naturel non nul), ça veut dire arriver à écrire  sous la forme
sous la forme 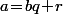 où
où  (=quotient) est un entier relatif et
(=quotient) est un entier relatif et  (=reste) est un entier tel que
(=reste) est un entier tel que  .
.
Le truc a savoir, c'est qu'une telle écriture est unique donc on peut employer absolument n'importe quelle méthode pour obtenir le résultat en question.
Une méthode classique consiste à écrire une série d'égalités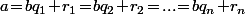 dans laquelle les
dans laquelle les 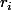 sont de plus en plus "petits" jusqu'à ce que le dernier
sont de plus en plus "petits" jusqu'à ce que le dernier 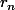 vérifie
vérifie  .
.
Comme ça reste très théorique, prenons l'exemple où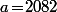 et
et 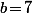 .
.
Tu as du apprendre dans le primaire à "poser" la division. Fait le (j'ai la flemme de l'écrire en MimeTeX vu que c'est un peu chiant de faire des tableaux).
Tu peut alors vérifier que ce que tu as fait, ça correspond précisément à écrire que
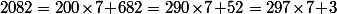
Et ce que je voulais "pointer du doigt", c'est qu'on aurait pu aller un peu plus vite en acceptant des "restes négatifs", par exemple, le premier truc qu'on a cherché à diviser, c'est 20 par 7 et on a dit qu'il y allait 2 fois et qu'il restait 6 : 20=2x7+6, mais comme il y va "presque" 3 fois, on pourrait songer à écrire à la place 20=3x7-1 qui n'est pas une "division euclidienne" mais qui donne un "reste" -1 plus petit en valeur absolue que le "vrai" reste égal à 6.
Si on revient à la division complète de 2082 par 7, ça correspond à écrire comme première étape que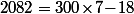 et on peut parfaitement continuer en effectuant la division de -18 par 7 qui est
et on peut parfaitement continuer en effectuant la division de -18 par 7 qui est 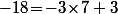 qui nous donne
qui nous donne 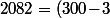\!\times\!7\!+\!3) .
.
Le seul truc auquel il faut faire un peu attention, c'est au fait que la division euclidienne de -18 par 7, ce n'est pas la même chose que celle de +18 par 7, mais même ça, ce n'est pas super grave vu que, si on avait écrit que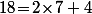 , ça aurait donné
, ça aurait donné 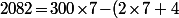\!=\!298\!\times\!7\!-\!4) qui ne correspond pas à la division euclidienne vu que le reste est <0, mais c'est facile à rectifier en écrivant que
qui ne correspond pas à la division euclidienne vu que le reste est <0, mais c'est facile à rectifier en écrivant que 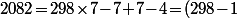\!\times\!7\!+\!(7\!-\!4)) .
.
Enfin bref, tout ce laïus pour dire qu'on peut faire un peu n'importe quoi, pourvu qu'a la dernière étape ait un reste tel que .
.
Pour en revenir à ton exercice où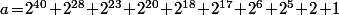 et
et 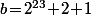 , quelle valeur très simple prendrait tu pour
, quelle valeur très simple prendrait tu pour 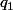 de façon à ce que
de façon à ce que 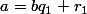 avec
avec 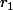 "plus petit" que
"plus petit" que  ?
?
Si tu préfère te poser la question différemment, on peut formuler ça en disant "ça vaut à peu prés combien la division de par
par  ?" (sans machine évidement)
?" (sans machine évidement)
Faire la "division Euclidienne" de
Le truc a savoir, c'est qu'une telle écriture est unique donc on peut employer absolument n'importe quelle méthode pour obtenir le résultat en question.
Une méthode classique consiste à écrire une série d'égalités
Comme ça reste très théorique, prenons l'exemple où
Tu as du apprendre dans le primaire à "poser" la division. Fait le (j'ai la flemme de l'écrire en MimeTeX vu que c'est un peu chiant de faire des tableaux).
Tu peut alors vérifier que ce que tu as fait, ça correspond précisément à écrire que
Et ce que je voulais "pointer du doigt", c'est qu'on aurait pu aller un peu plus vite en acceptant des "restes négatifs", par exemple, le premier truc qu'on a cherché à diviser, c'est 20 par 7 et on a dit qu'il y allait 2 fois et qu'il restait 6 : 20=2x7+6, mais comme il y va "presque" 3 fois, on pourrait songer à écrire à la place 20=3x7-1 qui n'est pas une "division euclidienne" mais qui donne un "reste" -1 plus petit en valeur absolue que le "vrai" reste égal à 6.
Si on revient à la division complète de 2082 par 7, ça correspond à écrire comme première étape que
Le seul truc auquel il faut faire un peu attention, c'est au fait que la division euclidienne de -18 par 7, ce n'est pas la même chose que celle de +18 par 7, mais même ça, ce n'est pas super grave vu que, si on avait écrit que
Enfin bref, tout ce laïus pour dire qu'on peut faire un peu n'importe quoi, pourvu qu'a la dernière étape ait un reste tel que
Pour en revenir à ton exercice où
Si tu préfère te poser la question différemment, on peut formuler ça en disant "ça vaut à peu prés combien la division de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 102 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
