On est demnader a determiner les premiers (P) positifs tels que :
P/[(3^P)+2) . (les P qui divisent (3^P)+2 en dautres termes . )
jusqu’à maintenant je sais que 3^P +2 est impair ce qui donne P>2 .
j’ai essayé de donner une forme générale des 3^n + 2 mais ca n’aboutit a rien .
je ne crois pas que le crible d’erathosténe puisse m’aider pour un encadrement plus précis de ces P.
Bref j’ai besoin d’aide par où commencer.
Arithmétique dans Z
3 messages
- Page 1 sur 1
Re: Arithmétique dans Z
Bonjour
Ton énoncé n'est pas clair. Si la formulation correcte c'est de déterminer les nombre premiers
p qui divisent 3^p+2 alors la réponse c'est que le seul qui répond à la question c'est p=5.
Ton énoncé n'est pas clair. Si la formulation correcte c'est de déterminer les nombre premiers
p qui divisent 3^p+2 alors la réponse c'est que le seul qui répond à la question c'est p=5.
Re: Arithmétique dans Z
Bonjour;
Soit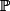 l'ensemble des nombres premiers .
l'ensemble des nombres premiers .
Soit .
.
Le petit théorème de Fermat donne : ; donc :
; donc :  ;
;
donc : ;
;
donc si divise
divise  ; alors
; alors  divise
divise  ; donc :
; donc : 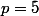 .
.
Soit
Soit
Le petit théorème de Fermat donne :
donc :
donc si
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
