Arithmétique - Carré parfait

[upium666]

Bonjour à tous et à toutes !

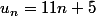
On définit la suite par pour tout entier naturel
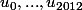
Parmi les termes , quels sont ceux qui sont des carrés parfaits ?

Merci

[upium666]

J'ai trouvé :

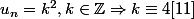
ou

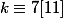
Mais je bloque

[Skullkid]

Bonsoir, regarde du côté de la réciproque de l'implication que tu as démontrée. Si k est congru à 4 modulo 11, à quelle condition sur n as-tu u_n = k^2 ? Même chose pour k congru à 7 modulo 11.

[upium666]

Bonsoir, regarde du côté de la réciproque de l'implication que tu as démontrée. Si k est congru à 4 modulo 11, à quelle condition sur n as-tu u_n = k^2 ? Même chose pour k congru à 7 modulo 11.

Bonjour,
Je le ferai quand j'aurai un petit moment
Mais je veux savoir : Ce que je viens de trouver n'est-il qu'un cas parmi les nombreuses conditions à trouver ?
Parce que je ne pense pas que les k correspondants ne soient QUE de la forme 11k+4 ou 11k+7

[chan79]

salut
Ce que tu as démontré, c'est que, si 11n+5 est un carré,

alors 11n+5 est de la forme (4+11p)² ou de la forme (7+11p)² avec p entier

Fais la réciproque en supposant d'abord que 11n+5=(4+11p)² et vois si ça te permet d'avoir un entier n.
Tu pourras lister les n qui conviennent entre 0 et 2012