Bonjour,
J'aimerai savoir les prérequis pour apprendre les exponentielle.
Je précise que j'étais bon en math au collège, ensuite je suis parti en lycée pro, les math étaient relativement simple et depuis j'ai lâché complètement cette matière, je ne me rappelle plus de rien.
En ce moment j'ai besoin d'apprendre les exponentielle, quels sont les sites que vous me conseillez et les prérequis à avoir ?
Apprendre les math exponentielle
7 messages
- Page 1 sur 1
Re: Apprendre les math exponentielle
tu veux apprendre l'exponentielle pour :
_ étudier le courbe ?
_ faire du calcul différentiel ?
_ en connaitre plus sur a exposant b quand b n'est pas un entier ?
Dans quel domaine, pour quelle utilisation en as-tu de besoin ?
_ étudier le courbe ?
_ faire du calcul différentiel ?
_ en connaitre plus sur a exposant b quand b n'est pas un entier ?
Dans quel domaine, pour quelle utilisation en as-tu de besoin ?
Re: Apprendre les math exponentielle
Je suis actuellement un cour sur le langage de programmation python, on apprend à se servir du module "math" et je suis tombé sur la fonction qui renvoie l'exponentielle d'un nombre.
Sauf que je ne sais pas ce que c'est, et je suis juste curieux de le savoir.
C'est donc plus de la curiosité, j'en ai pas réellement besoin en réalité.
ça change quelque chose ?
Sauf que je ne sais pas ce que c'est, et je suis juste curieux de le savoir.
C'est donc plus de la curiosité, j'en ai pas réellement besoin en réalité.
ça change quelque chose ?
Re: Apprendre les math exponentielle
version courbes en physique.
le log en base 10; c'est
log(10) = 1
log(100)=log(10*10)=2
log(1000)=log(10*10*10)=3
sa fonction inverse, c'est 10 exposant x
pour les fonctions mathématique, on utilise un ln, le logarithme népérien
avec e=2.7......
ln(e)=1
ln(e*e)=2
l(e*e*e)=3
la fonction exp, c'est l'inverse de ln, pour x strictement positif :
ln (x) =k <=> x=exp(k)
exp(k), c'est e exposant k, k peut être un nombre réel
Pourquoi ln et exp alors que log et 10 exposant x étaient bien ?
quand on aborde le traitement du signal, les dérivées et autres, ln et exp permettent des calculs plus simples et s'étendent aux nombres complexes pour résoudre efficacement les équations différentielles.
le log en base 10; c'est
log(10) = 1
log(100)=log(10*10)=2
log(1000)=log(10*10*10)=3
sa fonction inverse, c'est 10 exposant x
pour les fonctions mathématique, on utilise un ln, le logarithme népérien
avec e=2.7......
ln(e)=1
ln(e*e)=2
l(e*e*e)=3
la fonction exp, c'est l'inverse de ln, pour x strictement positif :
ln (x) =k <=> x=exp(k)
exp(k), c'est e exposant k, k peut être un nombre réel
Pourquoi ln et exp alors que log et 10 exposant x étaient bien ?
quand on aborde le traitement du signal, les dérivées et autres, ln et exp permettent des calculs plus simples et s'étendent aux nombres complexes pour résoudre efficacement les équations différentielles.
Re: Apprendre les math exponentielle
pascal16 a écrit:version courbes en physique.
le log en base 10; c'est
log(10) = 1
log(100)=log(10*10)=2
log(1000)=log(10*10*10)=3
sa fonction inverse, c'est 10 exposant x
pour les fonctions mathématique, on utilise un ln, le logarithme népérien
avec e=2.7......
ln(e)=1
ln(e*e)=2
l(e*e*e)=3
la fonction exp, c'est l'inverse de ln, pour x strictement positif :
ln (x) =k <=> x=exp(k)
exp(k), c'est e exposant k, k peut être un nombre réel
Pourquoi ln et exp alors que log et 10 exposant x étaient bien ?
quand on aborde le traitement du signal, les dérivées et autres, ln et exp permettent des calculs plus simples et s'étendent aux nombres complexes pour résoudre efficacement les équations différentielles.
C'est bien ce que je me disais, je n'ai absolument pas le niveau pour comprendre.
Si je veux vraiment apprendre un concept il faut bel et bien apprendre les math dans l'ordre, et non ce que j'ai envie.
Je dois tous reprendre depuis le début.
Re: Apprendre les math exponentielle
Une façon plus "intutive" de comprendre l'exponentielle, c'est de passer par les puissances.
Vous savez sûrement ce qu'est avec
avec  entier ; avec en particulier
entier ; avec en particulier 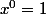
Passons aux puissances négatives:
Maintenant, les puissances rationnelles : il faut alors se protéger avec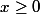 (car on va parler de racines carrées, ou racines
(car on va parler de racines carrées, ou racines  -ième et si
-ième et si  est pair cela ne marche pas bien pour les nombres négatifs...)
est pair cela ne marche pas bien pour les nombres négatifs...)
Passons aux puissances quelconques : à ce stade, je ne donnerai pas de preuve, mais intuitivement :
Par exemple,
et

(évidemment, ici on pourrait simplifier la fraction )
)
L'exponentielle est alors vue comme un certain nombre appelé , élevé à la puissance
, élevé à la puissance  :
: =e^x)
Le nombre étant une constante fondamentale, comme
étant une constante fondamentale, comme  :
:  . C'est un nombre irrationnel transcendant, comme
. C'est un nombre irrationnel transcendant, comme 
La propriété fondamentale mathématique de l'exponentielle est que la fonction est égale à sa dérivée.
La propriété fondamentale physique de l'exponentielle est que "pratiquement" tous les phénomènes physique suivent une évolution exponentielle : toute suite géométrique par exemple (capital placé à taux fixe, période de demi-vie des éléments radioactifs, réaction nucléaire en chaîne...)
Vous savez sûrement ce qu'est
Passons aux puissances négatives:
- comme la multiplication
est égale à
n cela nous amène à poser \dfrac{1}{x}=x^{-1} parce qu'ainsi on a
- comme
, on étend la notation
précédente à
Maintenant, les puissances rationnelles : il faut alors se protéger avec
- comme on a \sqrt x^2=x, si on pose \sqrt x=x^\alpha la règle \big(x^\alpha\big)^2=x^{2\alpha}=x^1 aboutit à \alpha=\dfrac{1}{2}
- cela se généralise à la racine
-ème de tout nombre positif :
- et on définit alors
Passons aux puissances quelconques : à ce stade, je ne donnerai pas de preuve, mais intuitivement :
- tout réel est la lmite d'une suite de Cauchy de rationnel
- (pour faire simple : tout réel est la limite de la suite formée par ses troncatures à la
-ième décimales, et cette troncature est évidemment un rationnel puisque c'est un décimal)
- En admettant que la limite se conserve bien comme il faut, on appelle
la limite de la suite
où
est une suite de Cauchy de rationnels de limite
Par exemple,
et
(évidemment, ici on pourrait simplifier la fraction
L'exponentielle est alors vue comme un certain nombre appelé
Le nombre
La propriété fondamentale mathématique de l'exponentielle est que la fonction est égale à sa dérivée.
La propriété fondamentale physique de l'exponentielle est que "pratiquement" tous les phénomènes physique suivent une évolution exponentielle : toute suite géométrique par exemple (capital placé à taux fixe, période de demi-vie des éléments radioactifs, réaction nucléaire en chaîne...)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Apprendre les math exponentielle
Bonjour,
En simplifié, les exponentielles sont la généralisation à tous les nombres des suites géométriques (suites telles que chaque terme de la suite est multiplié par un même nombre (sa raison) pour donner le suivant).
Par exemple, la suite géométrique de raison 2 et 1er terme 1 : 2^n=2.2.2.....2, compté n fois. On a 2^0=1, 2^1=2, 2^2=4, 2^3=8, etc... à chaque pas, on multiplie par 2. On dit que la croissance est exponentielle, car elle suit l'exposant "n".
On peut le faire avec 2, avec 3, ... 6,2, ... n'importe quel nombre (positif). Avec e=2,71..., la constante de Neper, c'est pratique pour les mathématiques. Alors l'exponentielle d'un nombre "x" est e^x. Par exemple l'exponentielle du nombre 3 est e^3 environ égal à 19,95.
Maintenant on peut aussi généraliser les exposants, comme l'a expliqué hdci, pour avoir une croissance (pour une raison > 1, décroissance pour une raison < 1) continue entre les points entiers.
Toujours est-il que la croissance "explose" (ou la décroissance "implose"). Car à chaque point, le taux d'accroissement d'un point à l'autre est égal à la valeur prise par le point. Pour en revenir à 2^n, le taux d'accroissement (variation des valeurs prises divisée par la variation de la variable) entre n et n+1 est égal à 2^n (par exemple entre n=2 et n=3, le taux d'accroissement est de (8-4)/(3-2)=4, entre 3 et 4 il est égal à 8...).
En simplifié, les exponentielles sont la généralisation à tous les nombres des suites géométriques (suites telles que chaque terme de la suite est multiplié par un même nombre (sa raison) pour donner le suivant).
Par exemple, la suite géométrique de raison 2 et 1er terme 1 : 2^n=2.2.2.....2, compté n fois. On a 2^0=1, 2^1=2, 2^2=4, 2^3=8, etc... à chaque pas, on multiplie par 2. On dit que la croissance est exponentielle, car elle suit l'exposant "n".
On peut le faire avec 2, avec 3, ... 6,2, ... n'importe quel nombre (positif). Avec e=2,71..., la constante de Neper, c'est pratique pour les mathématiques. Alors l'exponentielle d'un nombre "x" est e^x. Par exemple l'exponentielle du nombre 3 est e^3 environ égal à 19,95.
Maintenant on peut aussi généraliser les exposants, comme l'a expliqué hdci, pour avoir une croissance (pour une raison > 1, décroissance pour une raison < 1) continue entre les points entiers.
Toujours est-il que la croissance "explose" (ou la décroissance "implose"). Car à chaque point, le taux d'accroissement d'un point à l'autre est égal à la valeur prise par le point. Pour en revenir à 2^n, le taux d'accroissement (variation des valeurs prises divisée par la variation de la variable) entre n et n+1 est égal à 2^n (par exemple entre n=2 et n=3, le taux d'accroissement est de (8-4)/(3-2)=4, entre 3 et 4 il est égal à 8...).
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
