Angles orientés ~Chasles

[upium666]

Bonjour à tous et à toutes

Existe-t-il une application semblable à la relation de Chasles sur les vecteurs qui nous permette de décomposer les vecteurs et dans la formule suivante ?
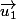
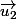
Donnée : =+ et =+


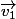
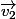
Merci

[Nightmare]

Qu'entends-tu par (u,v) ?

[upium666]

Qu'entends-tu par (u,v) ?

Peut-on "éjecter" les symboles "+" des couples de vecteurs ? (les décomposer)

[Nightmare]

Ok, j'ai lu le titre et je comprends qu'il s'agit d'angles orientés.

Alors non, il n'existe pas de formule simple, mais on peut toujours calculer à la main :

cos(u+v,w)=(u+v).w/(||u+v||.||w||)=1/||u+v|| (||u||cos((u,w))+||v||cos((v,w)))