Salut,
Avant tout BONNE ANNEE à tous/toutes :happy2:
J'ai besoin de votre aide pour cet exercice sur le thème de l'abscisse curviligne associé au cercle. Je vous sollicite surtout pour construire une démonstration, articulée autour de la cuisine de mes observations !
--- Enoncé :
On considère, sur un cercle orienté, tous les points dont l'abscisse curviligne

par rapport à une origine A est exprimée en radians par la relation (1) :

, dans laquelle on a
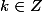
. Combien existe-t-il de points distincts sur le cercle ? Quelle est la nature du polygone dont ces points sont les sommets ?
Même questions pour la relation (2) :

.
--- Ma solution...
- Observations pour la relation (1) :

,
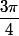
représente, suivant l'origine A, l'abscisse du 1er point/sommet d'un polygone et

le "motif" qui, suivant les valeurs de k, permet de construire les autres sommets de la figure. Cette valeur du motif me laisse penser à quatre sommets, c-a-d un carré inscrit dans un cercle, puisque pour
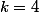
on a

, un tour complet sur le cercle.
Je continue ma "démonstration":
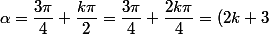\dfrac{\pi}{4})
, pour k=1, k=2, k=3, k=4 détermine un cycle de 4 abscisses curvilignes espacées de
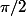
qui se répètent et se superposent dans un sens comme dans l'autre suivant le signe des valeurs de
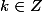
. CQFD ?
- Remarques pour la relation (2) :

,

représente, suivant l'origine A, l'abscisse curviligne du 1er point/sommet d'une figure.

ne forme pas la base d'un motif pour un polygone régulier, tout du moins sur l'intervalle
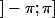
. Pour des valeurs de k>2 l'ensemble des points/sommets forment peut être une figure que je n'imagine pas... sauf si je savais la tracer simplement à l'aide de Geogebra, par exemple. Cependant, il est possible qu'une valeur de k soit la base d'un cycle qui se répète...
J'espère avoir était assez clair dans le déroulement de ma prose ? :doute:
Merci par avance pour vos réponses
@+
